
【题目】已知等边三角形![]() 的边长为
的边长为![]() ,
,![]() 为
为![]() 边的中点,沿
边的中点,沿![]() 将
将![]() 折成直二面角
折成直二面角![]() ,则三棱锥
,则三棱锥![]() 的外接球的表面积为_____
的外接球的表面积为_____
【答案】![]()
【解析】
先证明AD⊥平面BCD,利用二面角的定义得知∠BDC=90°,利用勾股定理可得出△BCD的外接圆直径为BC,设R为三棱锥A﹣BCD的外接球的半径,得![]() ,再利用球体表面积公式可得出答案.
,再利用球体表面积公式可得出答案.
如图所示,

折叠前,由于△ABC时等边三角形,D为BC的中点,则AD⊥BC,
折叠后,则有AD⊥CD,AD⊥BD,∵BD∩CD=D,∴AD⊥平面BCD,
∵二面角B﹣AD﹣C为直二面角,∵AD⊥BD,AD⊥CD,则二面角B﹣AD﹣C的平面角为∠BDC=90°,
且![]() ,
,
Rt△BCD的外接圆直径为![]() ,
,
所以,三棱锥A﹣BCD的外接球半径为![]() ,
,
因此,三棱锥A﹣BCD的外接球的表面积为4πR2=80π.
故答案为:80π


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() 是
是![]() 的导函数.
的导函数.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)设![]() .①若函数
.①若函数![]() 在定义域上单调递增,求
在定义域上单调递增,求![]() 的取值范围;②若函数
的取值范围;②若函数![]() 在定义域上不单调,试判定
在定义域上不单调,试判定![]() 的零点个数,并给出证明过程.
的零点个数,并给出证明过程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图、90后从事互联网行业者岗位分布条形图,则下列结论中一定正确的是( )
(注:90后指1990年及以后出生,80后指1980-1989年之间出生,80前指1979年及以前出生).


A.互联网行业从业人员中80前占3%以上
B.互联网行业90后中,从事设计岗位的人数比从事市场岗位的人数要多
C.互联网行业中从事技术岗位的人数超过总人数的20%
D.互联网行业中从事技术岗位的人数90后比80后多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知,图中直棱柱![]() 的底面是菱形,其中
的底面是菱形,其中![]() .又点
.又点![]() 分别在棱
分别在棱![]() 上运动,且满足:
上运动,且满足:![]() ,
,![]() .
.
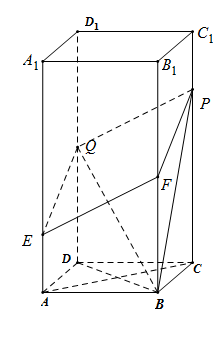
(1)求证:![]() 四点共面,并证明
四点共面,并证明![]() ∥平面
∥平面![]() .
.
(2)是否存在点![]() 使得二面角
使得二面角![]() 的余弦值为
的余弦值为![]() ?如果存在,求出
?如果存在,求出![]() 的长;如果不存在,请说明理由.
的长;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,已形成了全民自觉参与,造福百姓的良性循环.据此,某网站退出了关于生态文明建设进展情况的调查,调查数据表明,环境治理和保护问题仍是百姓最为关心的热点,参与调查者中关注此问题的约占![]() .现从参与关注生态文明建设的人群中随机选出200人,并将这200人按年龄分组:第1组
.现从参与关注生态文明建设的人群中随机选出200人,并将这200人按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
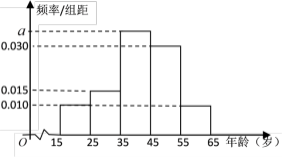
(I)求出![]() 的值;
的值;
(II)求出这200人年龄的样本平均数(同一组数据用该区间的中点值作代表)和中位数(精确到小数点后一位);
(III)现在要从年龄较小的第1,2组中用分层抽样的方法抽取5人,再从这5人中随机抽取3人进行问卷调查,求第2组恰好抽到2人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了让贫困地区的孩子们过一个温暖的冬天,某校阳光志愿者社团组织“这个冬天不再冷”冬衣募捐活动,共有50名志愿者参与.志愿者的工作内容有两项:①到各班做宣传,倡议同学们积极捐献冬衣;②整理、打包募捐上来的衣物.每位志愿者根据自身实际情况,只参与其中的某一项工作.相关统计数据如下表所示:

(1)如果用分层抽样的方法从参与两项工作的志愿者中抽取5人,再从这5人中选2人,那么“至少有1人是参与班级宣传的志愿者”的概率是多少?
(2)若参与班级宣传的志愿者中有12名男生,8名女生,从中选出2名志愿者,用![]() 表示所选志愿者中的女生人数,写出随机变量
表示所选志愿者中的女生人数,写出随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右两个焦点分别为
的左、右两个焦点分别为![]() ,离心率
,离心率![]() ,短轴长为2.
,短轴长为2.
(1)求椭圆的方程;
(2)点![]() 为椭圆上的一动点(非长轴端点),
为椭圆上的一动点(非长轴端点),![]() 的延长线与椭圆交于
的延长线与椭圆交于![]() 点,
点, ![]() 的延长线与椭圆交于
的延长线与椭圆交于![]() 点,求
点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com