
分析 把要求解的不等式变形,分子分母同时除以x后把$\frac{1}{x}$看作一个整体,由已知不等式的解集得到$\frac{1}{x}$的范围,进一步求出x的取值范围得答案.
解答 解:若x=0不符合题意,则x≠0,
由$\frac{b}{x+a}+\frac{cx+d}{dx+c}<0$$\frac{bx}{ax+1}+\frac{dx+c}{cx+d}<0$得,$\frac{b•\frac{1}{x}}{1+a•\frac{1}{x}}+\frac{c+d•\frac{1}{x}}{d+c•\frac{1}{x}}<0$,
即$\frac{b•\frac{1}{x}}{a•\frac{1}{x}+1}+\frac{d•\frac{1}{x}+c}{c•\frac{1}{x}+d}<0$,
设t=$\frac{1}{x}$,则不等式变为$\frac{bt}{at+1}+\frac{dt+c}{ct+d}<0$,
因为不等式$\frac{bx}{ax+1}$+$\frac{dx+c}{cx+d}$<0的解集为(-2,-1)∪($\frac{1}{3}$,1),
所以-2<$\frac{1}{x}$<-1或$\frac{1}{3}<$$\frac{1}{x}$<1,
解得-1<x<$-\frac{1}{2}$或1<x<3,
所以所求的不等式解集是$(-1,-\frac{1}{2})∪(1,3)$,
故答案为:$(-1,-\frac{1}{2})∪(1,3)$.
点评 本题考查不等式的解法,考查转化思想、整体思想,以及换元法的应用,是中档题.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
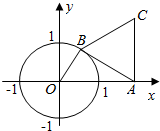 如图的平面直角坐标系中,O为坐标原点,点B在单位圆上,A(2,0),∠AOB=θ,△ABC为等边三角形.
如图的平面直角坐标系中,O为坐标原点,点B在单位圆上,A(2,0),∠AOB=θ,△ABC为等边三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{a}$与$\overrightarrow{b}$共线,$\overrightarrow{b}$与$\overrightarrow{c}$共线,则$\overrightarrow{a}$与$\overrightarrow{c}$也共线 | |
| B. | 任意两个相等的非零向量的始点与终点总是一平行四边形的四个顶点 | |
| C. | 向量$\overrightarrow{a}$与$\overrightarrow{b}$不共线,则$\overrightarrow{a}$与$\overrightarrow{b}$都是非零向量 | |
| D. | 有相同起点的两个非零向量不平行 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com