
已知三棱锥的顶点在底面内的射影为底面三角形的垂心,求证底面内任一顶点在其相对侧面内的射影也是此侧面三角形的垂心.
|
证明 如图,在三棱锥P-ABC中,P在底面内的射影O为△ABC的垂心,AO、CO分别交BC、AB于D、E.
由O为△ABC的垂心,知AO⊥BC. 由三垂线定理,可得BC⊥PA. 由BC⊥平面PAD,知BC⊥PD.
作AH⊥PD于H,则AH⊥平面PBC,即H为A在平面PBC内的射影. 由AH⊥平面PBC, 由三垂线定理,可知PC⊥AB,AB∩AH=A, 故PC⊥平面ABH,BH 由PH⊥BC,BH⊥PC,知H为△PBC的垂心. 同理可证B、C在其相对侧面内的射影也是侧面三角形PAC、PAB的垂心. 注意,复习、巩固上一单元的基础知识,也是学习本单元的目的之一. |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2014届重庆市高二12月月考理科数学试卷(解析版) 题型:选择题
已知三棱锥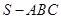 的各顶点都在一个半径为
的各顶点都在一个半径为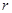 的球面上, 球心
的球面上, 球心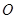 在
在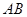 上,
上,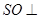 底面
底面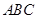 ,
,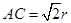 ,则球的体积与三棱锥体积之比是( )
,则球的体积与三棱锥体积之比是( )
A.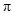 B.
B.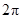 C.
C.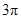 D.
D.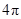
查看答案和解析>>
科目:高中数学 来源:2014届四川省高二10月月考理科数学试卷(解析版) 题型:选择题
已知三棱锥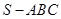 的各顶点都在一个半径为
的各顶点都在一个半径为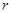 的球面上,球心
的球面上,球心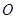 在
在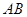 上,
上,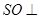 底面
底面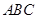 ,
,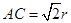 ,则球的体积与三棱锥体积之比是( )
,则球的体积与三棱锥体积之比是( )
A.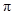 B.
B.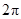 C.
C.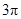 D.
D.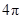
查看答案和解析>>
科目:高中数学 来源:2010-2011学年重庆市高三下学期第一次月考考试数学理卷 题型:填空题
已知三棱锥 的各顶点都在一个半径为
的各顶点都在一个半径为 的球面上,球心
的球面上,球心 在
在 上,
上, 底面
底面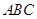 ,
, ,则三棱锥的体积与球的体积之比是 .
,则三棱锥的体积与球的体积之比是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com