
【题目】如图,椭圆![]()
![]() 过点
过点![]() ,其左、右焦点分别为
,其左、右焦点分别为![]() ,离心率
,离心率![]() ,
, ![]() 是椭圆右准线上的两个动点,且
是椭圆右准线上的两个动点,且![]() .
.
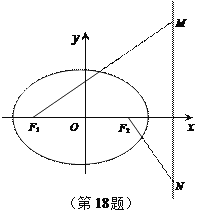
(1)求椭圆的方程;
(2)求![]() 的最小值;
的最小值;
(3)以![]() 为直径的圆
为直径的圆![]() 是否过定点?请证明你的结论.
是否过定点?请证明你的结论.
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)=2x﹣ ![]() .
.
(1)若f(x)= ![]() ,求x的值;
,求x的值;
(2)若2tf(2t)+mf(t)≥0对于t∈[1,2]恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个结论,其中正确的是( )
A.若 ![]() ,则a<b
,则a<b
B.“a=3“是“直线l1:a2x+3y﹣1=0与直线l2:x﹣3y+2=0垂直”的充要条件
C.在区间[0,1]上随机取一个数x,sin ![]() 的值介于0到
的值介于0到 ![]() 之间的概率是
之间的概率是 ![]()
D.对于命题P:?x∈R使得x2+x+1<0,则?P:?x∈R均有x2+x+1>0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=loga ![]() 是奇函数(其中a>1)
是奇函数(其中a>1)
(1)求m的值;
(2)判断f(x)在(2,+∞)上的单调性并证明;
(3)当x∈(r,a﹣2)时,f(x)的取值范围恰为(1,+∞),求a与r的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=lg[log ![]() (
( ![]() x﹣1)]的定义域为集合A,集合B={x|x<1,或x≥3}.
x﹣1)]的定义域为集合A,集合B={x|x<1,或x≥3}.
(1)求A∪B,(RB)∩A;
(2)若2a∈A,且log2(2a﹣1)∈B,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com