
【题目】已知函数![]()
(1)求函数的定义域;
(2)判定函数![]() 在
在![]() 的单调性,并证明你的结论;
的单调性,并证明你的结论;
(3)若当![]() 时,
时, ![]() 恒成立,求正整数
恒成立,求正整数![]() 的最大值.
的最大值.
【答案】(1)![]() (2)减函数 (3)3
(2)减函数 (3)3
【解析】试题分析:
(1)结合函数的解析式可得函数的定义域为![]() ;
;
(2)对函数 求导,结合题意和导函数的解析式可得![]() =-
=-![]()
![]() <0,所以函数f(x)在区间(-1,0)上是减函数.
<0,所以函数f(x)在区间(-1,0)上是减函数.
(3)首先由不等式的性质可得k的最大值不大于3,然后结合导函数的性质可得![]() 满足题意,即正整数
满足题意,即正整数![]() 的最大值是3.
的最大值是3.
试题解析:
解:(Ⅰ)函数的定义域为![]()
(Ⅱ)![]() =
=![]()
![]() =-
=-![]()
![]() 设
设![]() ,
,
故g(x)在(-1,0)上是减函数,而g(x)>g(0)=1>0,
故![]() =-
=-![]()
![]() <0,
<0,
所以函数f(x)在区间(-1,0)上是减函数.
(III)当x>0时,f(x)>![]() 恒成立, 令x=1有k<2
恒成立, 令x=1有k<2![]()
又k为正整数.∴k的最大值不大于3.
下面证明当k=3时,f(x)>![]() (x>0)恒成立.
(x>0)恒成立.
即证当x>0时, ![]()
![]() +1-2x>0恒成立.
+1-2x>0恒成立.
令g(x)=![]()
![]() +1-2x,则
+1-2x,则![]() =
=![]() -1,
-1,
当x>e-1时, ![]() >0;当0<x<e-1时,
>0;当0<x<e-1时, ![]() <0.
<0.
∴当x=e-1时,g(x)取得最小值g(e-1)=3-e>0.
∴当x>0时, ![]()
![]() +1-2x>0恒成立.
+1-2x>0恒成立.
因此正整数k的最大值为3.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】若函数![]() 满足下列条件:在定义域内存在
满足下列条件:在定义域内存在![]() ,使得
,使得![]() 成立,则称函数
成立,则称函数![]() 具有性质
具有性质![]() ;反之,若
;反之,若![]() 不存在,则称函数
不存在,则称函数![]() 不具有性质
不具有性质![]() .
.
(Ⅰ)证明:函数![]() 具有性质
具有性质![]() ,并求出对应的
,并求出对应的![]() 的值;
的值;
(Ⅱ)试分别探究形如①![]() (
(![]() )、②
)、②![]() (
(![]() 且
且![]() )、③
)、③![]() (
(![]() 且
且![]() )的函数,是否一定具有性质
)的函数,是否一定具有性质![]() ?并加以证明.
?并加以证明.
(Ⅲ)已知函数![]() 具有性质
具有性质![]() ,求
,求![]() 的取值范围;
的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某校新、老校区之间开车单程所需时间为![]() ,
, ![]() 只与道路畅通状况有关,对其容量为
只与道路畅通状况有关,对其容量为![]() 的样本进行统计,结果如图:
的样本进行统计,结果如图:
| 25 | 30 | 35 | 40 |
频数(次) | 20 | 30 | 40 | 10 |
(1)求![]() 的分布列与数学期望
的分布列与数学期望![]() ;
;
(2)刘教授驾车从老校区出发,前往新校区做一个50分钟的讲座,结束后立即返回老校区,求刘教授从离开老校区到返回老校区共用时间不超过120分钟的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,与
两点,与![]() 轴,
轴, ![]() 轴分别相交于点
轴分别相交于点![]() 和点
和点![]() ,且
,且![]() ,点
,点![]() 是点
是点![]() 关于
关于![]() 轴的对称点,
轴的对称点, ![]() 的延长线交椭圆于点
的延长线交椭圆于点![]() ,过点
,过点![]() 分别做
分别做![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() .
.
(1) 若椭圆![]() 的左、右焦点与其短轴的一个端点是正三角形的三个顶点,点
的左、右焦点与其短轴的一个端点是正三角形的三个顶点,点![]() 在椭圆
在椭圆![]() 上,求椭圆
上,求椭圆![]() 的方程;
的方程;
(2)当![]() 时,若点
时,若点![]() 平分线段
平分线段![]() ,求椭圆
,求椭圆![]() 的离心率.
的离心率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,我海监船在![]() 岛海域例行维权巡航,某时刻航行至
岛海域例行维权巡航,某时刻航行至![]() 处,此时测得其东北方向与它相距
处,此时测得其东北方向与它相距![]() 海里的
海里的![]() 处有一外国船只,且
处有一外国船只,且![]() 岛位于海监船正东
岛位于海监船正东![]() 海里处.
海里处.
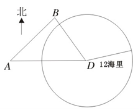
(1)求此时该外国船只与![]() 岛的距离;
岛的距离;
(2)观测中发现,此外国船只正以每小时![]() 海里的速度沿正南方向航行,为了将该船拦截在离
海里的速度沿正南方向航行,为了将该船拦截在离![]() 岛
岛![]() 海里处,不让其进入
海里处,不让其进入![]() 岛
岛![]() 海里内的海域,试确定海监船的航向,并求其速度的最小值.(参考数据:
海里内的海域,试确定海监船的航向,并求其速度的最小值.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某土特产销售总公司为了解其经营状况,调查了其下属各分公司月销售额和利润,得到数据如下表:
分公司名称 | 雅雨 | 雅鱼 | 雅女 | 雅竹 | 雅茶 |
月销售额 | 3 | 5 | 6 | 7 | 9 |
月利润额 | 2 | 3 | 3 | 4 | 5 |
在统计中发现月销售额![]() 和月利润额
和月利润额![]() 具有线性相关关系.
具有线性相关关系.
(1)根据如下的参考公式与参考数据,求月利润额![]() 与月销售额
与月销售额![]() 之间的线性回归方程;
之间的线性回归方程;
(2)若该总公司还有一个分公司“雅果”月销售额为10万元,试估计它的月利润额是多少?
(参考公式: 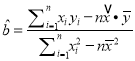 ,
, ![]() ,其中:
,其中: ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
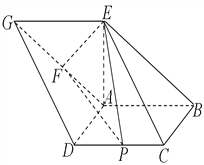
【题目】如图,已知四边形![]() 和
和![]() 均为平行四边形,点
均为平行四边形,点![]() 在平面
在平面![]() 内的射影恰好为点
内的射影恰好为点![]() ,以
,以![]() 为直径的圆经过点
为直径的圆经过点![]() ,
, ![]() ,
, ![]() 的中点为
的中点为![]() ,
, ![]() 的中点为
的中点为![]() ,且
,且![]() .
.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求几何体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位:cm).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布![]() .
.
(1)假设生产状态正常,记X表示一天内抽取的16个零件中其尺寸在![]()
之外的零件数,求![]() ;
;
(2)一天内抽检零件中,如果出现了尺寸在![]() 之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
下面是检验员在一天内抽取的16个零件的尺寸:
9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
经计算得![]() ,
, 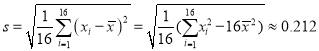 ,其中
,其中![]() 为抽取的第
为抽取的第![]() 个零件的尺寸,
个零件的尺寸, ![]() .
.
用样本平均数![]() 作为
作为![]() 的估计值
的估计值![]() ,用样本标准差
,用样本标准差![]() 作为
作为![]() 的估计值
的估计值![]() ,利用估计值判断是否需对当天的生产过程进行检查?剔除
,利用估计值判断是否需对当天的生产过程进行检查?剔除![]() 之外的数据,用剩下的数据估计
之外的数据,用剩下的数据估计![]() 和
和![]() (精确到0.01).
(精确到0.01).
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,
![]() ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com