
【题目】已知实数![]() ,设函数
,设函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,若对任意的
时,若对任意的![]() ,均有
,均有![]() ,求
,求![]() 的取值范围.
的取值范围.
注:![]() 为自然对数的底数.
为自然对数的底数.
【答案】(1)![]() 在
在![]() 内单调递减,在
内单调递减,在![]() 内单调递增;(2)
内单调递增;(2)![]()
【解析】
(1)求导后取出极值点,再分![]() ,
,![]() 两种情况进行讨论即可.
两种情况进行讨论即可.
(2)当![]() 时得出
时得出![]() 的一个取值范围,再讨论
的一个取值范围,再讨论![]() 时的情况,再对
时的情况,再对![]() 时构造函数两边取对数进行分析论证
时构造函数两边取对数进行分析论证![]() 时
时![]() 恒成立.
恒成立.
(1)由![]() ,解得
,解得![]() .
.
①若![]() ,则当
,则当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 内单调递增;
内单调递增;
当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 内单调递减.
内单调递减.
②若![]() ,则当
,则当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 内单调递增;
内单调递增;
当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 内单调递减.
内单调递减.
综上所述,![]() 在
在![]() 内单调递减,在
内单调递减,在![]() 内单调递增.
内单调递增.
(2)![]() ,即
,即![]() .
.
令![]() ,得
,得![]() ,则
,则![]() .
.
当![]() 时,不等式
时,不等式![]() 显然成立,
显然成立,
当![]() 时,两边取对数,即
时,两边取对数,即![]() 恒成立.
恒成立.
令函数![]() ,即
,即![]() 在
在![]() 内恒成立.
内恒成立.
由![]() ,得
,得![]() .
.
故当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() 单调递减.
单调递减.
因此![]() .
.
令函数![]() ,其中
,其中![]() ,
,
则![]() ,得
,得![]() ,
,
故当![]() 时,
时,![]() ,
,![]() 单调递减;当
单调递减;当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
又![]() ,
,![]() ,
,
故当![]() 时,
时,![]() 恒成立,因此
恒成立,因此![]() 恒成立,
恒成立,
即当![]() 时,对任意的
时,对任意的![]() ,均有
,均有![]() 成立.
成立.


科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 是函数
是函数![]() 的反函数,解方程
的反函数,解方程![]() ;
;
(2)当![]()
![]() 时,定义
时,定义![]() ,设
,设![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,求
,求![]() 及
及![]() ;
;
(3)对于任意![]() ,其中
,其中![]() ,当
,当![]() 能作为一个三角形的三边长时,
能作为一个三角形的三边长时,![]() 也总能作为一个三角形的三边长,试探究M的最小值.
也总能作为一个三角形的三边长,试探究M的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 与直线
与直线![]() 有且只有一个交点,点P为椭圆C上任一点,
有且只有一个交点,点P为椭圆C上任一点,![]() ,
,![]() .若
.若![]() 的最小值为
的最小值为![]() .
.
(1)求椭圆C的标准方程;
(2)设直线![]() 与椭圆C交于不同两点A,B,点O为坐标原点,且
与椭圆C交于不同两点A,B,点O为坐标原点,且![]() ,当
,当![]() 的面积S最大时,求
的面积S最大时,求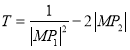 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】地球上的风能取之不尽,用之不竭.风能是淸洁能源,也是可再生能源.世界各国致力于发展风力发电,近10年来,全球风力发电累计装机容量连年攀升,中国更是发展迅猛,2014年累计装机容量就突破了![]() ,达到
,达到![]() ,中国的风力发电技术也日臻成熟,在全球范围的能源升级换代行动中体现出大国的担当与决心.以下是近10年全球风力发电累计装机容量与中国新增装机容量图. 根据所给信息,正确的统计结论是( )
,中国的风力发电技术也日臻成熟,在全球范围的能源升级换代行动中体现出大国的担当与决心.以下是近10年全球风力发电累计装机容量与中国新增装机容量图. 根据所给信息,正确的统计结论是( )
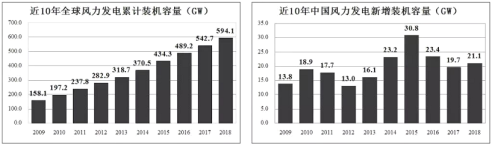
A.截止到2015年中国累计装机容量达到峰值
B.10年来全球新增装机容量连年攀升
C.10年来中国新增装机容量平均超过![]()
D.截止到2015年中国累计装机容量在全球累计装机容量中占比超过![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,离心率为
,离心率为![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() 为椭圆
为椭圆![]() 上的三点,
上的三点,![]() 与
与![]() 交于点
交于点![]() ,且
,且![]() ,当
,当![]() 的中点恰为点
的中点恰为点![]() 时,判断
时,判断![]() 的面积是否为常数,并说明理由.
的面积是否为常数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“绿水青山就是金山银山”的生态文明发展理念已经深入人心,这将推动新能源汽车产业的迅速发展.下表是近几年我国某地区新能源乘用车的年销售量与年份的统计表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
销量(万台) | 8 | 10 | 13 | 25 | 24 |
某机构调查了该地区30位购车车主的性别与购车种类情况,得到的部分数据如下表所示:
购置传统燃油车 | 购置新能源车 | 总计 | |
男性车主 | 6 | 24 | |
女性车主 | 2 | ||
总计 | 30 |
(1)求新能源乘用车的销量![]() 关于年份
关于年份![]() 的线性相关系数
的线性相关系数![]() ,并判断
,并判断![]() 与
与![]() 是否线性相关;
是否线性相关;
(2)请将上述![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为购车车主是否购置新能源乘用车与性别有关;
的把握认为购车车主是否购置新能源乘用车与性别有关;
(3)若以这30名购车车主中购置新能源乘用车的车主性别比例作为该地区购置新能源乘用车的车主性别比例,从该地区购置新能源乘用车的车主中随机选取50人,记选到女性车主的人数为X,求X的数学期望与方差.
参考公式: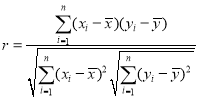 ,
,![]() ,其中
,其中![]() .
.![]() ,若
,若![]() ,则可判断
,则可判断![]() 与
与![]() 线性相关.
线性相关.
附表:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点P到直线![]() 的距离与到点
的距离与到点![]() 的距离之比为
的距离之比为![]() .
.
(1)求动点P的轨迹![]() ;
;
(2)直线![]() 与曲线
与曲线![]() 交于不同的两点A,B(A,B在
交于不同的两点A,B(A,B在![]() 轴的上方)
轴的上方)![]() :
:
①当A为椭圆与![]() 轴的正半轴的交点时,求直线
轴的正半轴的交点时,求直线![]() 的方程;
的方程;
②对于动直线![]() ,是否存在一个定点,无论
,是否存在一个定点,无论![]() 如何变化,直线
如何变化,直线![]() 总经过此定点?若存在,求出该定点的坐标;若不存在,请说明理由.
总经过此定点?若存在,求出该定点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com