
【题目】函数![]() ,则下列结论错误的是( )
,则下列结论错误的是( )
A. ![]() 是偶函数 B.
是偶函数 B. ![]() 的值域是
的值域是![]()
C. 方程![]() 的解只有
的解只有![]() D. 方程
D. 方程![]() 的解只有
的解只有![]()
【答案】C
【解析】
根据相关知识对给出的四个选项分别进行分析、判断后可得结论.
对于A,当![]() 为有理数时,有
为有理数时,有![]() ;当
;当![]() 为无理数时,有
为无理数时,有![]() ,所以函数为偶函数,所以A正确.
,所以函数为偶函数,所以A正确.
对于B,由题意得函数的值域为![]() ,所以B正确.
,所以B正确.
对于C,若![]() 为有理数,则方程f(f(x))=f(1)=1=f(x)恒成立;若
为有理数,则方程f(f(x))=f(1)=1=f(x)恒成立;若![]() 为无理数,则方程f(f(x))=f(0)=1≠f(x),此时无满足条件的x,故方程f(f(x))=f(x)的解为任意有理数,所以C不正确.
为无理数,则方程f(f(x))=f(0)=1≠f(x),此时无满足条件的x,故方程f(f(x))=f(x)的解为任意有理数,所以C不正确.
对于D,若x为有理数,则方程f(f(x))=f(1)=1,此时x=1;若x为无理数,则方程f(f(x))=f(0)=1,此时无满足条件的x,故方程f(f(x))=x的解为x=1,所以D正确.
故选C.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】为了了解湖南各景点在大众中的熟知度,随机对15~65岁的人群抽样了n人,回答问题“湖南省有哪几个著名的旅游景点?”统计结果如下图表.
组号 | 分组 | 回答正确的人数 | 回答正确的人数 |
第1组 | [15,25) | a | 0.5 |
第2组 | [25,35) | 18 | x |
第3组 | [35,45) | b | 0.9 |
第4组 | [45,55) | 9 | 0.36 |
第5组 | [55,65] | 3 | y |
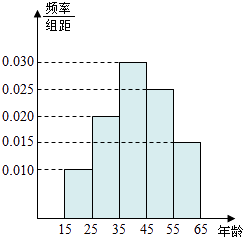
(1)分别求出a,b,x,y的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,求第2,3,4组每组各抽取多少人?
(3)在(2)抽取的6人中随机抽取2人,求所抽取的人中恰好没有第3组人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设顶点在原点,焦点在![]() 轴上的拋物线过点
轴上的拋物线过点![]() ,过
,过![]() 作抛物线的动弦
作抛物线的动弦![]() ,
, ![]() ,并设它们的斜率分别为
,并设它们的斜率分别为![]() ,
, ![]() .
.
(Ⅰ)求拋物线的方程;
(Ⅱ)若![]() ,求证:直线
,求证:直线![]() 的斜率为定值,并求出其值;
的斜率为定值,并求出其值;
(III)若![]() ,求证:直线
,求证:直线![]() 恒过定点,并求出其坐标.
恒过定点,并求出其坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题![]() 方程
方程![]() 表示双曲线;命题
表示双曲线;命题![]() 不等式
不等式![]() 的解集是
的解集是![]() .
. ![]() 为假,
为假, ![]() 为真,求
为真,求![]() 的取值范围.
的取值范围.
【答案】![]()
【解析】试题分析:由命题![]() 方程
方程![]() 表示双曲线,求出
表示双曲线,求出![]() 的取值范围,由命题
的取值范围,由命题![]() 不等式
不等式![]() 的解集是
的解集是![]() ,求出
,求出![]() 的取值范围,由
的取值范围,由![]() 为假,
为假, ![]() 为真,得出
为真,得出![]() 一真一假,分两种情况即可得出
一真一假,分两种情况即可得出![]() 的取值范围.
的取值范围.
试题解析:
![]() 真
真 ![]()
![]() ,
,
![]() 真
真 ![]() 或
或![]()
![]()
∴![]()
![]() 真
真![]() 假
假 ![]()
![]() 假
假![]() 真
真 ![]()
∴![]() 范围为
范围为![]()
【题型】解答题
【结束】
18
【题目】如图,设![]() 是圆
是圆![]() 上的动点,点
上的动点,点![]() 是
是![]() 在
在![]() 轴上的投影,
轴上的投影, ![]() 为
为![]() 上一点,且
上一点,且![]() .
.

(1)当![]() 在圆上运动时,求点
在圆上运动时,求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)求过点![]() 且斜率为
且斜率为![]() 的直线被
的直线被![]() 所截线段的长度.
所截线段的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设椭圆的中心为原点![]() ,长轴在
,长轴在![]() 轴上,上顶点为
轴上,上顶点为![]() ,左,右焦点分别为
,左,右焦点分别为![]() ,线段
,线段![]() 的中点分别为
的中点分别为![]() ,且
,且![]() 是面积为4的直角三角形.
是面积为4的直角三角形.
(1)求该椭圆的离心率和标准方程;
(2)过![]() 做直线
做直线![]() 交椭圆于
交椭圆于![]() 两点,使
两点,使![]() ,求直线
,求直线![]() 的方程.
的方程.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,曲线 ![]() 的极坐标方程是
的极坐标方程是 ![]() ,以极点为原点
,以极点为原点 ![]() ,极轴为
,极轴为 ![]() 轴正半轴(两坐标系取相同的单位长度)的直角坐标系
轴正半轴(两坐标系取相同的单位长度)的直角坐标系 ![]() 中,曲线
中,曲线 ![]() 的参数方程为:
的参数方程为: ![]() (
( ![]() 为参数).
为参数).
(1)求曲线 ![]() 的直角坐标方程与曲线
的直角坐标方程与曲线 ![]() 的普通方程;
的普通方程;
(2)将曲线 ![]() 经过伸缩变换
经过伸缩变换 ![]() 后得到曲线
后得到曲线 ![]() ,若
,若 ![]() 分别是曲线
分别是曲线 ![]() 和曲线
和曲线 ![]() 上的动点,求
上的动点,求 ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某产品生产厂家生产一种产品,每生产这种产品![]()
![]() (百台),其总成本为
(百台),其总成本为![]() 万元
万元![]() ,其中固定成本为42万元,且每生产1百台的生产成本为15万元
,其中固定成本为42万元,且每生产1百台的生产成本为15万元![]() 总成本
总成本![]() 固定成本
固定成本![]() 生产成本
生产成本![]() 销售收入
销售收入![]() 万元
万元![]() 满足
满足![]() ,假定该产品产销平衡
,假定该产品产销平衡![]() 即生产的产品都能卖掉
即生产的产品都能卖掉![]() ,根据上述条件,完成下列问题:
,根据上述条件,完成下列问题:
![]() 写出总利润函数
写出总利润函数![]() 的解析式
的解析式![]() 利润
利润![]() 销售收入
销售收入![]() 总成本
总成本![]() ;
;
![]() 要使工厂有盈利,求产量
要使工厂有盈利,求产量![]() 的范围;
的范围;
![]() 工厂生产多少台产品时,可使盈利最大?
工厂生产多少台产品时,可使盈利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的偶函数,且x≤0时, f(x)=-x+1
(1)求f(0),f(2);
(2)求函数f(x)的解析式;
(3)若f(a-1)<3,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com