
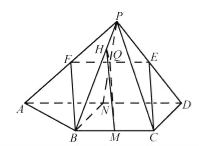
【题目】(本题满分15分)如图,已知四棱锥P–ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.

(Ⅰ)证明:CE∥平面PAB;
(Ⅱ)求直线CE与平面PBC所成角的正弦值.
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】本题主要考查空间点、线、面位置关系,直线与平面学科&网所成的角等基础知识,同时考查空间想象能力和运算求解能力。满分15分。
(Ⅰ)如图,设PA中点为F,连结EF,FB.
因为E,F分别为PD,PA中点,所以EF∥AD且![]() ,
,
又因为BC∥AD,![]() ,所以
,所以
EF∥BC且EF=BC,
即四边形BCEF为平行四边形,所以CE∥BF,
因此CE∥平面PAB.
(Ⅱ)分别取BC,AD的中点为M,N.连结PN交EF于点Q,连结MQ.
因为E,F,N分别是PD,PA,AD的中点,所以Q为EF中点,
在平行四边形BCEF中,MQ∥CE.
由△PAD为等腰直角三角形得
PN⊥AD.
由DC⊥AD,N是AD的中点得
BN⊥AD.
所以 AD⊥平面PBN,
由BC∥AD得 BC⊥平面PBN,
那么,平面PBC⊥平面PBN.
过点Q作PB的垂线,垂足为H,连结MH.
MH是MQ在平面PBC上的射影,所以∠QMH是直线CE与平面PBC所成的角.
设CD=1.
在△PCD中,由PC=2,CD=1,PD=![]() 得CE=
得CE=![]() ,
,
在△PBN中,由PN=BN=1,PB=![]() 得QH=
得QH=![]() ,
,
在Rt△MQH中,QH=![]() ,MQ=
,MQ=![]() ,
,
所以sin∠QMH=![]() ,
,
所以,直线CE与平面PBC所成角的正弦值是![]() .
.


科目:高中数学 来源: 题型:
【题目】函数f(x)=x2+ax+3.
(1)当x∈R时,f(x)≥a恒成立,求a的取值范围.
(2)当x∈[﹣2,2]时,f(x)≥a恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2 ![]() sinxcosx+2cos2x﹣1(x∈R) (Ⅰ)求函数f(x)的最小正周期及在区间[0,
sinxcosx+2cos2x﹣1(x∈R) (Ⅰ)求函数f(x)的最小正周期及在区间[0, ![]() ]上的最大值和最小值;
]上的最大值和最小值;
(Ⅱ)若f(x0)= ![]() ,x0∈[
,x0∈[ ![]() ,
, ![]() ],求cos2x0的值.
],求cos2x0的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=x2﹣ax+a(x∈R)同时满足:
①不等式f(x)≤0的解集有且只有一个元素;
②在定义域内存在0<x1<x2 , 使得不等式f(x1)>f(x2)成立.设数列{an}的前n项和Sn=f(n).
(1)求f(x)的表达式;
(2)求数列{an}的通项公式;
(3)设 ![]() ,cn=
,cn= ![]() ,{cn}的前n项和为Tn , 若Tn>2n+t对任意n∈N,n≥2恒成立,求实数t的取值范围.
,{cn}的前n项和为Tn , 若Tn>2n+t对任意n∈N,n≥2恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系内,设M(x1 , y1)、N(x2 , y2)为不同的两点,直线l的方程为ax+by+c=0,设 ![]() .有下列四个说法:
.有下列四个说法:
①存在实数δ,使点N在直线l上;
②若δ=1,则过M、N两点的直线与直线l平行;
③若δ=﹣1,则直线l经过线段MN的中点;
④若δ>1,则点M、N在直线l的同侧,且直线l与线段MN的延长线相交.
上述说法中,所有正确说法的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)与直线x+y﹣1=0相交于A、B两点,若a∈[
=1(a>b>0)与直线x+y﹣1=0相交于A、B两点,若a∈[ ![]() ,
, ![]() ],且以AB为直径的圆经过坐标原点O,则椭圆离心率e的取值范围为 .
],且以AB为直径的圆经过坐标原点O,则椭圆离心率e的取值范围为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题: ①函数f(x)=x+ ![]() 的最小值为6;
的最小值为6;
②不等式 ![]() <1的解集是{x|﹣1<x<1};
<1的解集是{x|﹣1<x<1};
③若a>b>﹣1,则 ![]() >
> ![]() ;
;
④若a>b,c>d,则ac>bd.
所有正确命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题一定正确的是( )
A.在等差数列{an}中,若ap+aq=ar+aδ , 则p+q=r+δ
B.已知数列{an}的前n项和为Sn , 若{an}是等比数列,则Sk , S2k﹣Sk , S3k﹣S2k也是等比数列
C.在数列{an}中,若ap+aq=2ar , 则ap , ar , aq成等差数列
D.在数列{an}中,若ap?aq=a ![]() ,则ap , ar , aq成等比数列
,则ap , ar , aq成等比数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若△ABC的内角A,B,C所对的边分别为a,b,c,且满足asinB﹣ ![]() bcosA=0
bcosA=0
(1)求A;
(2)当a= ![]() ,b=2时,求△ABC的面积.
,b=2时,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com