练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某企业生产甲、乙两种产品均需用A，B两种原料．已知生产1吨每种产品所需原料及每天原料的可用限额如表所示．如果生产一吨甲、乙产品可获得利润分别为3万元、4万元，则该企业每天可获得最大利润为（ ）

    甲

    乙

    原料限额

    A（吨）

    3

    2

    12

    B（吨）

    1

    2

    8


    A.12万元
    B.16万元
    C.17万元
    D.18万元

    【答案】D
    【解析】解：设每天生产甲乙两种产品分别为x，y吨，利润为z元，
    则 ，
    目标函数为 z=3x+4y．
    作出二元一次不等式组所表示的平面区域（阴影部分）即可行域．
    由z=3x+4y得y=﹣ x+ ，
    平移直线y=﹣ x+ 由图象可知当直线y=﹣ x+ 经过点B时，直线y=﹣ x+ 的截距最大，
    此时z最大，
    解方程组 ，解得 ，
    即B的坐标为x=2，y=3，
    ∴zmax=3x+4y=6+12=18．
    即每天生产甲乙两种产品分别为2，3吨，能够产生最大的利润，最大的利润是18万元，
    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥S﹣ABCD的底面是正方形，SA⊥底面ABCD，E是SC上一点．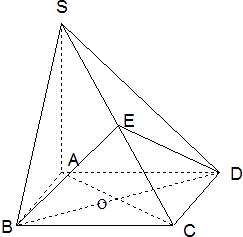

    （1）求证：平面EBD⊥平面SAC；
    （2）设SA=4，AB=2，求点A到平面SBD的距离；
    （3）设SA=4，AB=2，当OE丄SC时，求二面角E﹣BD﹣C余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 ，其中a为常数．
    （1）若a=1，判断函数f（x）的奇偶性；
    （2）若函数 在其定义域上是奇函数，求实数a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知f（x）=x5 +bx﹣8，且f（﹣2）=10，则f（2）=（ ）
    A.﹣26
    B.﹣18
    C.﹣10
    D.10

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=loga（3﹣ax）．
    （1）当 时，函数f（x）恒有意义，求实数a的取值范围；
    （2）是否存在这样的实数a，使得函数f（x）在区间[2，3]上为增函数，并且f（x）的最大值为1．如果存在，试求出a的值；如果不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设实数x，y满足条件 ，若目标函数z=ax+by（a＞0，b＞0）的最大值为12，则 的最小值为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，内角A，B，C的对边分别为a，b，c，已知2ccosA+a=2b．
    （1）求角C的值；
    （2）若a+b=4，当c取最小值时，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=lnx，则函数g（x）=f（x）﹣f′（x）的零点所在的区间是（ ）
    A.（0，1）
    B.（1，2）
    C.（2，3）
    D.（3，4）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=（ + ）x3（a＞0且a≠1）．
    （1）求函数f（x）的定义域；
    （2）讨论函数f（x）的奇偶性；
    （3）求a的取值范围，使f（x）＞0在定义域上恒成立．

    查看答案和解析>>

    同步练习册答案