
【题目】某学校餐厅新推出A、B、C、D四款套餐,某一天四款套餐销售情况的条形图如下.为了了解同学对新推出的四款套餐的评价,对每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:
满意 | 一般 | 不满意 | |
A套餐 | 50% | 25% | 25% |
B套餐 | 80% | 0 | 20% |
C套餐 | 50% | 50% | 0 |
D套餐 | 40% | 20% | 40% |
(Ⅰ)若同学甲选择的是A款套餐,求甲的调查问卷被选中的概率;
(Ⅱ)若想从调查问卷被选中且填写不满意的同学中再选出2人进行面谈,求这两人中至少有一人选择的是D款套餐的概率.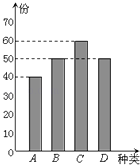
【答案】解:(Ⅰ)由条形图可得,选择A,B,C,D四款套餐的学生共有200人, 其中选A款套餐的学生为40人,
由分层抽样可得从A款套餐问卷中抽取了 ![]() 份.
份.
设事件M=“同学甲被选中进行问卷调查”,
则 ![]() .
.
答:若甲选择的是A款套餐,甲被选中调查的概率是0.1.
(II) 由图表可知,选A,B,C,D四款套餐的学生分别接受调查的人数为4,5,6,5.其中不满意的人数分别为1,1,0,2个.
记对A款套餐不满意的学生是a;对B款套餐不满意的学生是b;对D款套餐不满意的学生是c,d.
设事件N=“从填写不满意的学生中选出2人,至少有一人选择的是D款套餐”
从填写不满意的学生中选出2人,共有(a,b),(a,c),(a,d),(b,c),(b,d),(c,d)6个基本事件,
而事件N有(a,c),(a,d),(b,c),(b,d),(c,d)5个基本事件,
则 ![]() .
.
答:这两人中至少有一人选择的是D款套餐的概率是 ![]()
【解析】(I)由条形图可得,选择A,B,C,D四款套餐的学生共有200人,其中选A款套餐的学生为40人,由分层抽样可得从A款套餐问卷中抽取的人数.(II)由图表可知,选A,B,C,D四款套餐的学生分别接受调查的人数为4,5,6,5.其中不满意的人数分别为1,1,0,2个,做出所有的事件和满足条件的事件数,得到概率.
【考点精析】认真审题,首先需要了解频率分布直方图(频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息).


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)=lnx,g(x)=(2﹣a)(x﹣1)﹣2f(x). (Ⅰ)当a=1时,求函数g(x)的单调区间;
(Ⅱ)设F(x)=|f(x)|+ ![]() (b>0).对任意x1 , x2∈(0,2],x1≠x2 , 都有
(b>0).对任意x1 , x2∈(0,2],x1≠x2 , 都有 ![]() <﹣1,求实数b的取值范围.
<﹣1,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xoy中,曲线C1: ![]() (t为参数,t≠0),其中0≤α<π,在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=2sinθ,曲线C3:ρ=2
(t为参数,t≠0),其中0≤α<π,在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=2sinθ,曲线C3:ρ=2 ![]() cosθ. (Ⅰ)求C2与C3交点的直角坐标;
cosθ. (Ⅰ)求C2与C3交点的直角坐标;
(Ⅱ)若C2与C1相交于点A,C3与C1相交于点B,求|AB|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中政教处为了调查学生对“一带一路”的关注情况,在全校组织了“一带一路知多少”的知识问卷测试,并从中随机抽取了12份问卷,得到其测试成绩(百分制)的茎叶图如下:.

(1)写出该样本的中位数,若该校共有3000名学生,试估计该校测试成绩在70分以上的人数;
(2)从所抽取的70分以上的学生中再随机选取4人,记![]() 表示测试成绩在80分以上的人数,求
表示测试成绩在80分以上的人数,求![]() 的分布列和数学期望
的分布列和数学期望
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() =(2,﹣
=(2,﹣ ![]() ),
), ![]() =(sin2(
=(sin2( ![]() +x),cos2x).令f(x)=
+x),cos2x).令f(x)= ![]()
![]() ﹣1,x∈R,函数g(x)=f(x+φ),φ∈(0,
﹣1,x∈R,函数g(x)=f(x+φ),φ∈(0, ![]() )的图象关于(﹣
)的图象关于(﹣ ![]() ,0)对称. (Ⅰ) 求f(x)的解析式,并求φ的值;
,0)对称. (Ⅰ) 求f(x)的解析式,并求φ的值;
(Ⅱ)在△ABC中sinC+cosC=1﹣ ![]() ,求g(B)的取值范围.
,求g(B)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设Sn是数列{an}的前n项和,已知a1=3,an+1=2Sn+3(n∈N) (I)求数列{an}的通项公式;
(Ⅱ)令bn=(2n﹣1)an , 求数列{bn}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com