
分析 通过基本不等式$\frac{a+b}{2}$≥$\frac{2}{\frac{1}{a}+\frac{1}{b}}$可知$\frac{1}{a}$+$\frac{1}{b}$≥4•$\frac{1}{a+b}$,利用对称性相加即得结论.
解答 证明:∵a>0,b>0,c>0,
∴$\frac{a+b}{2}$≥$\frac{2}{\frac{1}{a}+\frac{1}{b}}$,
∴$\frac{1}{a}$+$\frac{1}{b}$≥4•$\frac{1}{a+b}$,
同理可知$\frac{1}{b}$+$\frac{1}{c}$≥4•$\frac{1}{b+c}$,
$\frac{1}{c}$+$\frac{1}{a}$≥4•$\frac{1}{c+a}$,
三式相加可知:2($\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{c}$)≥4($\frac{1}{a+b}$+$\frac{1}{b+c}$+$\frac{1}{c+a}$),
∴$\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{c}$≥2($\frac{1}{a+b}$+$\frac{1}{b+c}$+$\frac{1}{c+a}$).
点评 本题考查不等式的证明,利用基本不等式是解决本题的关键,注意解题方法的积累,属于中档题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
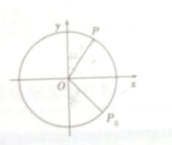 如图,质点P在半径为2的圆周上逆时针运动,其初始位置为P0($\sqrt{2}$,-$\sqrt{2}$),角速度为1,点P到x轴的距离d是关于时间t的函数,当t=$\frac{π}{4}$时,d=0.
如图,质点P在半径为2的圆周上逆时针运动,其初始位置为P0($\sqrt{2}$,-$\sqrt{2}$),角速度为1,点P到x轴的距离d是关于时间t的函数,当t=$\frac{π}{4}$时,d=0.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com