
【题目】如图1所示,在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的平分线,点
的平分线,点![]() 在线段
在线段![]() 上,
上, ![]() .如图2所示,将
.如图2所示,将![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() ,连结
,连结![]() ,设点
,设点![]() 是
是![]() 的中点.
的中点.
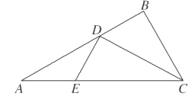

图1 图2
(1)求证: ![]() 平面
平面![]() ;
;
(2)在图2中,若![]() 平面
平面![]() ,其中
,其中![]() 为直线
为直线![]() 与平面
与平面![]() 的交点,求三棱锥
的交点,求三棱锥![]() 的体积.
的体积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,证明
,证明![]() ,利用平面与平面垂直的性质证明
,利用平面与平面垂直的性质证明![]() 平面
平面![]() ;(2)过点
;(2)过点![]() 作
作![]() 交于点
交于点![]() ,因为平面
,因为平面![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,求得
,求得![]() ,利用棱锥的体积公式,即可求三棱锥
,利用棱锥的体积公式,即可求三棱锥![]() 的体积.
的体积.
试题解析:(1)在题图1中,因为![]() ,
, ![]() ,
, ![]() ,所以
,所以![]() .
.
因为![]() 为
为![]() 的平分线,所以
的平分线,所以![]() ,
,
所以![]() .
.
又因为![]() ,
, ![]() ,所以
,所以![]()
则![]() ,所以
,所以![]() ,即
,即![]()
在题图2中,因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
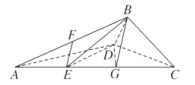
(2)在题图2中,因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]()
因为点![]() 在线段
在线段![]() 上,
上, ![]() ,点
,点![]() 是
是![]() 的中点,所以
的中点,所以![]()
过点![]() 作
作![]() 交于点
交于点![]()
因为平面![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]()
由条件得![]()
又![]()
![]() ,
,
所以三棱锥![]() 的体积为
的体积为![]()
![]() .
.
【方法点晴】本题主要考查线面垂直的判定定理及面面垂直的性质、棱锥的体积公式,属于难题.解答空间几何体中垂直关系时,一般要根据已知条件把空间中的线线、线面、面面之间垂直关系进行转化,转化时要正确运用有关的定理,找出足够的条件进行推理;证明直线和平面垂直的常用方法有:(1)利用判定定理;(2)利用判定定理的推论![]() ;(3)利用面面平行的性质
;(3)利用面面平行的性质![]() ;(4)利用面面垂直的性质,当两个平面垂直时,在一个平面内垂直于交线的直线垂直于另一个平面.
;(4)利用面面垂直的性质,当两个平面垂直时,在一个平面内垂直于交线的直线垂直于另一个平面.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 、
、![]() 为椭圆
为椭圆![]() :
: ![]() (
(![]() )的左、右焦点,点
)的左、右焦点,点![]() 为椭圆上一点,且
为椭圆上一点,且![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若圆![]() 是以
是以![]() 为直径的圆,直线
为直径的圆,直线![]() :
: ![]() 与圆
与圆![]() 相切,并与椭圆
相切,并与椭圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 过两点
过两点![]() ,
, ![]() ,且圆心
,且圆心![]() 在直线
在直线![]() 上.
上.
(Ⅰ)求圆![]() 的标准方程;
的标准方程;
(Ⅱ)直线![]() 过点
过点![]() 且与圆
且与圆![]() 有两个不同的交点
有两个不同的交点![]() ,
, ![]() ,若直线
,若直线![]() 的斜率
的斜率![]() 大于0,求
大于0,求![]() 的取值范围;
的取值范围;
(Ⅲ)在(Ⅱ)的条件下,是否存在直线![]() 使得弦
使得弦![]() 的垂直平分线过点
的垂直平分线过点![]() ,若存在,求出直线
,若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过点![]() 的直线与圆
的直线与圆![]() 相切,且与直线
相切,且与直线![]() 垂直,则
垂直,则![]() ( )
( )
A. 2 B. 1 C. ![]() D.
D. ![]()
【答案】A
【解析】因为点P(2,2)满足圆![]() 的方程,所以P在圆上,
的方程,所以P在圆上,
又过点P(2,2)的直线与圆![]() 相切,且与直线axy+1=0垂直,
相切,且与直线axy+1=0垂直,
所以切点与圆心连线与直线axy+1=0平行,
所以直线axy+1=0的斜率为: ![]() .
.
故选A.
点睛:对于直线和圆的位置关系的问题,可用“代数法”或“几何法”求解,直线与圆的位置关系体现了圆的几何性质和代数方法的结合,“代数法”与“几何法”是从不同的方面和思路来判断的,解题时不要单纯依靠代数计算,若选用几何法可使得解题过程既简单又不容易出错.
【题型】单选题
【结束】
23
【题目】设![]() 分别是双曲线
分别是双曲线![]() 的左、右焦点.若点
的左、右焦点.若点![]() 在双曲线上,且
在双曲线上,且![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两圆![]() ,
, ![]() 的圆心分别为c1,c2,,P为一个动点,且
的圆心分别为c1,c2,,P为一个动点,且![]() .
.
(1)求动点P的轨迹方程;
(2)是否存在过点A(2,0)的直线l与轨迹M交于不同的两点C,D,使得C1C=C1D?若存在,求出直线l的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校射击队的某一选手射击一次,其命中环数的概率如表:
命中环数 | 10环 | 9环 | 8环 | 7环 |
概率 | 0.32 | 0.28 | 0.18 | 0.12 |
求该选手射击一次,
(1)命中9环或10环的概率.
(2)至少命中8环的概率.
(3)命中不足8环的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为圆
为圆![]() 的圆心,
的圆心, ![]() 是圆上动点,点
是圆上动点,点![]() 在圆的半径
在圆的半径![]() 上,且有点
上,且有点![]() 和
和![]() 上的点
上的点![]() ,满足
,满足![]()
(1)当![]() 在圆上运动时,求点
在圆上运动时,求点![]() 的轨迹方程;
的轨迹方程;
(2)若斜率为![]() 的直线
的直线![]() 与圆
与圆![]() 相切,与(1)中所求点
相切,与(1)中所求点![]() 的轨迹教育不同的两点
的轨迹教育不同的两点![]()
![]() 是坐标原点,且
是坐标原点,且![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015年12月,华中地区数城市空气污染指数“爆表”,此轮污染为2015年以来最严重的污染过程,为了探究车流量与![]() 的浓度是否相关,现采集到华中某城市2015年12月份某星期星期一到星期日某一时间段车流量与
的浓度是否相关,现采集到华中某城市2015年12月份某星期星期一到星期日某一时间段车流量与![]() 的数据如表:
的数据如表:

(1)由散点图知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;(提示数据:
的线性回归方程;(提示数据: ![]() )
)
(2)利用(1)所求的回归方程,预测该市车流量为12万辆时![]() 的浓度.
的浓度.
参考公式:回归直线的方程是![]() ,其中
,其中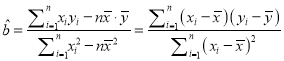 ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com