
【题目】已知点Q(ρ,θ),分别按下列条件求出点P的极坐标.
(1)点P是点Q关于极点O的对称点;
(2)点P是点Q关于直线θ= ![]() 的对称点.
的对称点.
【答案】
(1)
【解答】解:由于P,Q关于极点对称,得极径|OP|=|OQ|,极角相差(2k+1)π(k∈Z).所以,点P的极坐标为(ρ,(2k+1)π+θ)或(-ρ,2kπ+θ)(k∈Z).
(2)
【解答】解:由P,Q关于直线θ= ![]() 对称,得它们的极径|OP|=|OQ|,点P的极角θ′满足θ′=π-θ+2kπ(k∈Z),
对称,得它们的极径|OP|=|OQ|,点P的极角θ′满足θ′=π-θ+2kπ(k∈Z),
所以点P的坐标为(ρ,(2k+1)π-θ)或(-ρ,2kπ-θ)(k∈Z).
【解析】本题主要考查了,解决问题的关键是根据确定一点的极坐标关键是确定它的极径和极角两个量,为此应明确它们的含义.
【考点精析】认真审题,首先需要了解极坐标系(平面内取一个定点O,叫做极点;自极点O引一条射线OX叫做极轴;再选定一个长度单位、一个角度单位(通常取弧度)及其正方向(通常取逆时针方向),这样就建立了一个极坐标系).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(1+x),g(x)=loga(1﹣x),其中(a>0且a≠1),设h(x)=f(x)﹣g(x).
(1)求h(x)的定义域;
(2)判断h(x)的奇偶性,并说明理由;
(3)若a=log327+log2,求使f(x)>1成立的x的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂产生的废气经过过滤后排放,排放时污染物的含量不得超过1%.已知在过滤过程中废气中的污染物数量P(单位:毫克/升)与过滤时间t(单位:小时)之间的函数关系为:P=P0e﹣kt , (k,P0均为正的常数).若在前5个小时的过滤过程中污染物被排除了90%.那么,至少还需( )时间过滤才可以排放.
A.![]() 小时
小时
B.![]() 小时
小时
C.5小时
D.10小时
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)=2x-![]() .
.
(Ⅰ)若f(x)=![]() ,求x的值;
,求x的值;
(Ⅱ)若2tf(2t)+mf(t)≥0对于t∈[1,2]恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两支球队进行总决赛,比赛采用七场四胜制,即若有一队先胜四场,则此队为总冠军,比赛就此结束.因两队实力相当,每场比赛两队获胜的可能性均为![]() .据以往资料统计,第一场比赛可获得门票收入40万元,以后每场比赛门票收入比上一场增加10万元.
.据以往资料统计,第一场比赛可获得门票收入40万元,以后每场比赛门票收入比上一场增加10万元.
(I)求总决赛中获得门票总收入恰好为300万元的概率;
(II)设总决赛中获得门票总收入为X,求X的均值E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂用鲜牛奶在某台设备上生产A,B两种奶制品.生产1吨A产品需鲜牛奶2吨,使用设备1小时,获利1 000元;生产1吨B产品需鲜牛奶1.5吨,使用设备1.5小时,获利1 200元.要求每天B产品的产量不超过A产品产量的2倍,设备每天生产A,B两种产品时间之和不超过12小时.假定每天可获取的鲜牛奶数量W(单位:吨)是一个随机变量,其分布列为
W | 12 | 15 | 18 |
P | 0.3 | 0.5 | 0.2 |
该厂每天根据获取的鲜牛奶数量安排生产,使其获利最大,因此每天的最大获利Z(单位:元)是一个随机变量.
(I)求Z的分布列和均值;
(II)若每天可获取的鲜牛奶数量相互独立,求3天中至少有1天的最大获利超过10 000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
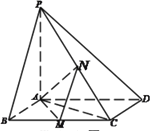
【题目】如图,已知四棱锥![]() ,底面
,底面![]() 为菱形,
为菱形,![]() ,
,![]() ,
, ![]() 平面
平面![]() ,
, ![]() 分别是
分别是![]() 的中点。
的中点。
(1)证明: ![]() ;
;
(2)若![]() 为
为![]() 的中点时,
的中点时,![]() 与平面
与平面![]() 所成的角最大,且所成角的正切值为
所成的角最大,且所成角的正切值为![]() ,求点A到平面
,求点A到平面![]() 的距离。
的距离。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医疗研究所为了检验某种血清预防感冒的作用,把500名使用血清的人与另外500名未使用血清的人一年中的感冒记录作比较,提出假设H:“这种血清不能起到预防感冒的作用”,利用2×2列联表计算的K2≈3.918,经查临界值表知P(K2≥3.841)≈0.05.则下列表述中正确的是( )
A.有95℅的把握认为“这种血清能起到预防感冒的作用”
B.若有人未使用该血清,那么他一年中有95℅的可能性得感冒
C.这种血清预防感冒的有效率为95℅
D.这种血清预防感冒的有效率为5℅
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com