
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() ,判断函数
,判断函数![]() 的单调性并说明理由;
的单调性并说明理由;
(2)若![]() ,求证:关
,求证:关![]() 的不等式
的不等式![]() 在
在![]() 上恒成立.
上恒成立.
科目:高中数学 来源: 题型:
【题目】(多选题)下列说法中,正确的命题是( )
A.已知随机变量![]() 服从正态分布
服从正态分布![]() ,
,![]() ,则
,则![]() .
.
B.以模型![]() 去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设![]() ,将其变换后得到线性方程
,将其变换后得到线性方程![]() ,则
,则![]() ,
,![]() 的值分别是
的值分别是![]() 和0.3.
和0.3.
C.已知两个变量具有线性相关关系,其回归直线方程为![]() ,若
,若![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
D.若样本数据![]() ,
,![]() ,…,
,…,![]() 的方差为2,则数据
的方差为2,则数据![]() ,
,![]() ,…,
,…,![]() 的方差为16.
的方差为16.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() ,
,![]() ,
,![]() .
.
(1)设![]() ,假设
,假设![]() 在
在![]() 上递减,求
上递减,求![]() 的取值范围;
的取值范围;
(2)假设![]() ,求证:
,求证:![]() .
.
(3)是否存在实数![]() ,使得
,使得![]() 恒成立,假设存在,求出
恒成立,假设存在,求出![]() 的取值范围,假设不存在,请说明理由.
的取值范围,假设不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)求函数![]() 的单调增区间;
的单调增区间;
(2)令![]() ,且函数
,且函数![]() 有三个彼此不相等的零点
有三个彼此不相等的零点![]() ,其中
,其中![]() .
.
①若![]() ,求函数
,求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
②若对![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产的产品中分正品与次品,正品重![]() ,次品重
,次品重![]() ,现有5袋产品(每袋装有10个产品),已知其中有且只有一袋次品(10个产品均为次品)如果将5袋产品以1~5编号,第
,现有5袋产品(每袋装有10个产品),已知其中有且只有一袋次品(10个产品均为次品)如果将5袋产品以1~5编号,第![]() 袋取出
袋取出![]() 个产品(
个产品(![]() ),并将取出的产品一起用秤(可以称出物体重量的工具)称出其重量
),并将取出的产品一起用秤(可以称出物体重量的工具)称出其重量![]() ,若次品所在的袋子的编号是2,此时的重量
,若次品所在的袋子的编号是2,此时的重量![]() _________
_________![]() ;若次品所在的袋子的编号是
;若次品所在的袋子的编号是![]() ,此时的重量
,此时的重量![]() _______
_______![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴的建立极坐标系,曲线
轴正半轴为极轴的建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程;
的普通方程;
(2)若点![]() 与点
与点![]() 分别为曲线
分别为曲线![]() 动点,求
动点,求![]() 的最小值,并求此时的
的最小值,并求此时的![]() 点坐标.
点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】博览会安排了分别标有序号为“1号”“2号”“3号”的三辆车,等可能随机顺序前往酒店接嘉宾.某嘉宾突发奇想,设计两种乘车方案.方案一:不乘坐第一辆车,若第二辆车的车序号大于第一辆车的车序号,就乘坐此车,否则乘坐第三辆车;方案二:直接乘坐第一辆车.记方案一与方案二坐到“3号”车的概率分别为P1,P2,则( )
A. P1P2=![]() B. P1=P2=
B. P1=P2=![]() C. P1+P2=
C. P1+P2=![]() D. P1<P2
D. P1<P2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,线段
,线段![]() 、
、![]() 都是圆
都是圆![]() 的弦,且
的弦,且![]() 与
与![]() 垂直且相交于坐标原点
垂直且相交于坐标原点![]() ,如图所示,设△
,如图所示,设△![]() 的面积为
的面积为![]() ,设△
,设△![]() 的面积为
的面积为![]() .
.
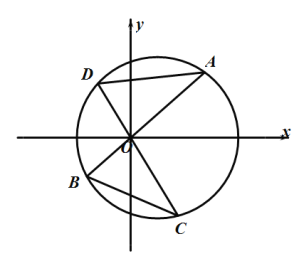
(1)设点![]() 的横坐标为
的横坐标为![]() ,用
,用![]() 表示
表示![]() ;
;
(2)求证:![]() 为定值;
为定值;
(3)用![]() 、
、![]() 、
、![]() 、
、![]() 表示出
表示出![]() ,试研究
,试研究![]() 是否有最小值,如果有,求出最小值,并写出此时直线
是否有最小值,如果有,求出最小值,并写出此时直线![]() 的方程;若没有最小值,请说明理由.
的方程;若没有最小值,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com