
设函数 (1)设
(1)设 的内角,且为钝角,求
的内角,且为钝角,求 的最小值;
的最小值;
(2)设 是锐角
是锐角 的内角,且
的内角,且 求
求 的三个内角的大小和AC边的长。
的三个内角的大小和AC边的长。
(1)最小值为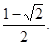 (2)
(2)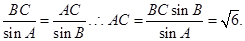
解析试题分析:(1)利用诱导公式和二倍角公式对函数解析式整理,进而根据A的范围,利用正弦函数的性质求得函数的最大和最小值.
(2)利用f(A)=1求得A,进而利用∠A+∠B的值求得B,进而根据三角形内角和求得C,最后利用正弦定理求得AC.
解:(1)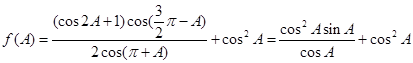
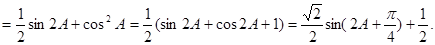 ………3分
………3分
∵角A为钝角,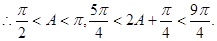 ……………………………4分
……………………………4分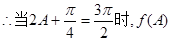 取值最小值,其最小值为
取值最小值,其最小值为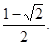 ……………………6分
……………………6分
(2)由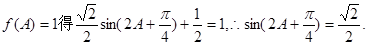 ………………8分
………………8分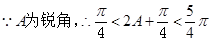 ,
,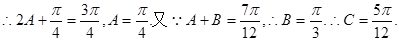 …………10分
…………10分
在△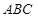 中,由正弦定理得:
中,由正弦定理得: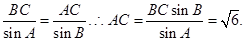 ……12分
……12分
考点:本题主要考查了三角函数的最值问题,正弦定理的应用.考查了综合分析问题的能力和基本的运算能力.
点评:解决该试题的关键是能够利用正弦定理和二倍角公式化简表达式得到三角函数的性质的熟练运用。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
(本题满分14分)已知函数 (其中
(其中 )的图象与
)的图象与 轴的交点中,相邻两个交点之间的距离为
轴的交点中,相邻两个交点之间的距离为 ,且图象上一个点为
,且图象上一个点为 .
.
(1)求 的解析式;
的解析式;
(2)若 求函数
求函数 的值域;
的值域;
(3)将函数 的图象向左平移
的图象向左平移 个单位,再将图象上各点的横坐标变为原来的2倍,纵坐标不变,求经以上变换后得到的函数解析式.
个单位,再将图象上各点的横坐标变为原来的2倍,纵坐标不变,求经以上变换后得到的函数解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com