练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知f(n)=(2n+7)·3n+9,存在自然数m,使得对任意n∈N,都能使m整除f(n)，则最大的m的值为


    1. A.
      30
    2. B.
      26
    3. C.
      36
    4. D.
      6
    C
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知f(n)=(2n+7)·3n+9,存在自然数m,使得对任意n∈N,都能使m整除f(n)，求m的最大值。

    查看答案和解析>>

    科目：高中数学 来源：2010-2011年辽宁省瓦房店市高二4月月考数学理卷 题型：选择题

    已知f(n)=(2n+7)·3n+9,存在自然数m,使得对任意n∈N,都能使m整除f(n)，则最大的m的值为(    )

    A、30           B、 26              C、 36          D、 6

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知f(n)=(2n+7)·3n+9，是否存在自然数m，使得对任意n∈N+,都能使m整除f(n),如果存在，求出最大的m值，并证明你的结论；若不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知f(n)=(2n+7)·3n+9,存在自然数m，使得对任意n∈N*，都能使m整除f(n)，求最大的m的值.

    查看答案和解析>>

    科目：高中数学 来源：2013届安徽省高二下学期期中考试理科数学试卷（解析版） 题型：解答题

    已知f(n)=(2n+7)3n+9,存在自然数m,使得对任意正整数n,都能使m整除f(n)，猜测出最大的m的值。并用数学归纳法证明你的猜测是正确的。

    【解析】本试题主要考查了归纳猜想的运用，以及数学归纳法的证明。

    ∵f(1)=36,f(2)=108=3×36,f(3)=360=10×36

    ∴f(1),f(2),f(3)能被36整除，猜想f(n)能被36整除

    然后证明n=1,2时，由上得证，设n=k(k≥2)时，

    f(k)=(2k+7)·3k+9能被36整除，则n=k+1时，

    f(k+1)－f(k)=(2k+9)·3k+1?－(2k+7)·3k=(6k+27)·3k－(2k+7)·3k

    =(4k+20)·3k=36(k+5)·3k－2?(k≥2)  证明得到。解析  ∵f(1)=36,f(2)=108=3×36,f(3)=360=10×36

    ∴f(1),f(2),f(3)能被36整除，猜想f(n)能被36整除 

    证明  n=1,2时，由上得证，设n=k(k≥2)时，

    f(k)=(2k+7)·3k+9能被36整除，则n=k+1时，

    f(k+1)－f(k)=(2k+9)·3k+1?－(2k+7)·3k=(6k+27)·3k－(2k+7)·3k

    =(4k+20)·3k=36(k+5)·3k－2?(k≥2) 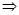 f(k+1)能被36整除

    ∵f(1)不能被大于36的数整除，∴所求最大的m值等于36

     

    查看答案和解析>>

    同步练习册答案