
【题目】《汉字听写大会》不断创收视新高,为了避免“书写危机”弘扬传统文化,某市对全市10万名市民进行了汉字听写测试,调查数据显示市民的成绩服从正态分布![]() .现从某社区居民中随机抽取50名市民进行听写测试,发现被测试市民正确书写汉字的个数全部在160到184之间,将测试结果按如下方式分成六组:第一组
.现从某社区居民中随机抽取50名市民进行听写测试,发现被测试市民正确书写汉字的个数全部在160到184之间,将测试结果按如下方式分成六组:第一组![]() ,第二组
,第二组![]() ,…,第六组
,…,第六组![]() ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.
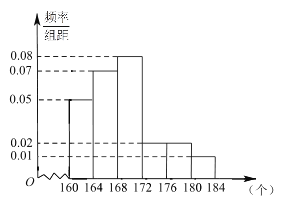
(1)试评估该社区被测试的50名市民的成绩在全市市民中成绩的平均状况及这50名市民成绩在172个以上(含172个)的人数;
(2)在这50名市民中成绩在172个以上(含172个)的人中任意抽取2人,该2人中成绩排名(从高到低)在全市前130名的人数记为![]() ,求
,求![]() 的数学期望.
的数学期望.
参考数据:若![]() ~
~![]() ,则
,则![]() ,
, ![]() ,
, ![]() .
.
【答案】(1)平均值168,人数10(2)![]() ,
,
【解析】试题分析:(1)根据组中值与对应区间概率乘积的和为平均值求平均数,根据直方图中小长方形面积等于对应区间概率求概率,再根据频数等于总数与概率乘积得人数(2)先确定随机变量取法,再分别求对应概率 列表得分布列,最后根据数学期望公式求期望
试题解析:(Ⅰ)由直方图,经过计算该社区50名市民的平均成绩为![]() ,高于全市的平均值168(或者:经过计算该社区居民平均成绩为168.72,比较接近全市的平均值168.
,高于全市的平均值168(或者:经过计算该社区居民平均成绩为168.72,比较接近全市的平均值168.
由频率分布直方图知,后三组频率为(0.02+0.02+0.01)×4=0.2,人数为0.2×50=10,即这50名市民成绩在172个以上(含172 个)的人数为10人.
(Ⅱ)∵P(168﹣3×4≤ξ<168+3×4)=0.9974,∴![]() ,0.0013×100 000=130.
,0.0013×100 000=130.
所以,全市前130名的成绩在180个以上(含180个),这50人中成绩在180 个以上(含180个)的有2人.随机变量ξ可取0,1,2,
于是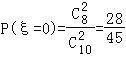 ,
,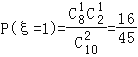 ,
,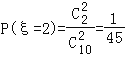 ,
,
∴![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x),当x,y∈R时,恒有f(x+y)=f(x)+f(y).当x>0时,f(x)>0
(1)求证:f(x)是奇函数;
(2)若 ![]() ,试求f(x)在区间[﹣2,6]上的最值;
,试求f(x)在区间[﹣2,6]上的最值;
(3)是否存在m,使f(2( ![]() )2﹣4)+f(4m﹣2(
)2﹣4)+f(4m﹣2( ![]() ))>0对任意x∈[1,2]恒成立?若存在,求出实数m的取值范围;若不存在,说明理由.
))>0对任意x∈[1,2]恒成立?若存在,求出实数m的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ ![]() ax2+(1﹣a)x,其中a∈R,f(x)的导函数是f′(x).
ax2+(1﹣a)x,其中a∈R,f(x)的导函数是f′(x).
(1)求函数f(x)的极值;
(2)在曲线y=f(x)的图象上是否存在不同的两点A(x1 , y1),B(x2 , y2)(x1≠x2),使得直线AB的斜率k=f′( ![]() )?若存在,求出x1与x2的关系;若不存在,请说明理由.
)?若存在,求出x1与x2的关系;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(1﹣x)+loga(x+3),其中0<a<1.
(1)求函数f(x)的定义域;
(2)若函数f(x)的最小值为﹣4,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学餐饮中心为了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查 结果如下表所示:
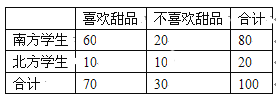
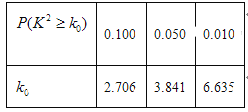
(1)根据表中数据,问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
(2)已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
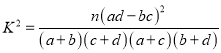 ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解甲、乙两个班级某次考试的数学成绩(单位:分),从甲、乙两个班级中分别随机抽取5名学生的成绩作样本,如图是样本的茎叶图,规定:成绩不低于120分时为优秀成绩. 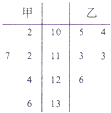
(1)从甲班的样本中有放回的随机抽取2个数据,求其中只有一个优秀成绩的概率;
(2)从甲、乙两个班级的样本中分别抽取2名学生的成绩,记获优秀成绩的总人数为X,求X的分布列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com