
|
| 2y |
| x+1 |
|
| 2y |
| x+1 |
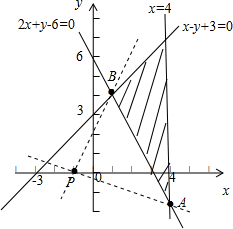 解:作出约束条件
解:作出约束条件
|
| 2y |
| x+1 |
|
|
| 2 |
| 5 |
| 2y |
| x+1 |
| 4 |
| 5 |
| 4 |
| 5 |


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:
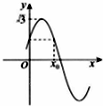 已知f(x)=Asin(2x+
已知f(x)=Asin(2x+| π |
| 6 |
| π |
| 4 |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| lnx+k |
| ex |
| e-2+1 |
| x2+x |
查看答案和解析>>
科目:高中数学 来源: 题型:
 |
| y |
 |
| a |
| x | 16 | 17 | 18 | 19 |
| y | 50 | 34 | 41 | 31 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 1000 |
查看答案和解析>>
科目:高中数学 来源: 题型:

| A、f(x)-①,g(x)-②,h(x)-③,φ(x)-④ |
| B、f(x)-①,φ(x)-②,g(x)-③,h(x)-④ |
| C、g(x)-①,h(x)-②,f(x)-③,φ(x)-④ |
| D、f(x)-①,h(x)-②,g(x)-③,φ(x)-④ |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| y2 |
| b2 |
| x2 |
| a2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
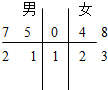 某校高三年级共有300人参加数学期中考试,从中随机抽取4名男生和4名女生的试卷,获得某一道题的样本,该题得分的茎叶图如图.
某校高三年级共有300人参加数学期中考试,从中随机抽取4名男生和4名女生的试卷,获得某一道题的样本,该题得分的茎叶图如图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com