已知集合A={x|x2+2x+p=0},B={y|y=x2,x≠0},若A∩B=∅,求实数p的取值范围.
解:∵y=x
2,x≠0
∴y>0
∴B=(0,+∞)
∵A∩B=∅
∴A=∅或A⊆(-∞,0]
即方程x
2+2x+p=0无实根或无正实根
(1)当方程x
2+2x+p=0无实根时,
有△=4-4p<0,即p>1
(2)当方程x
2+2x+p=0无正实根时,
有
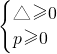
,即0≤p≤1
综上所述:p>1 或0≤p≤1
分析:先利用二次函数的特点求得B=(0,+∞),根据A∩B=∅?方程x
2+2x+p=0无实根或无正实根,(1)当方程x
2+2x+p=0无实根时,
有△=4-4p<0,即p>1;(2)当方程x
2+2x+p=0无正实根时,有
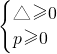
,即0≤p≤1.
点评:本题考查了交集及其运算以及一元二次方程根的情况,要注意A∩B=∅的含义,属于基础题.

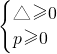 ,即0≤p≤1
,即0≤p≤1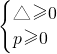 ,即0≤p≤1.
,即0≤p≤1.
