
设函数f(θ)= sinθ+cosθ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
sinθ+cosθ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
(1)若点P的坐标为 ,求f(θ)的值;
,求f(θ)的值;
(2)若点P(x,y)为平面区域Ω: ,上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
,上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
(1)2;(2)0≤θ≤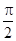 ; f(θ)的最大值等于2 ,f(θ)最小值等于1.
; f(θ)的最大值等于2 ,f(θ)最小值等于1.
【解析】
试题分析:(1)由任意角三角函数的定义可得sinθ,cosθ,代入函数f(θ)= sinθ+cosθ,从而求出f(θ)的值.
sinθ+cosθ,从而求出f(θ)的值.
(2)作出平面区域Ω(即三角区域ABC),如图所示,其点P在该平面区域内,连结OP,便可得角θ的范围.将f(θ)化一得: f(θ)= sinθ+cosθ=2sin(θ+
sinθ+cosθ=2sin(θ+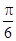 ).根据角θ的范围,结合正弦函数的图象的性质,便 可得f(θ)的范围.
).根据角θ的范围,结合正弦函数的图象的性质,便 可得f(θ)的范围.
试题解析:(1)由点P的坐标和三角函数的定义可得sinθ= ,cosθ=
,cosθ=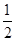 .
.
于是f(θ)= sinθ+cos θ=
sinθ+cos θ=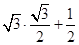 =2.
=2.
(2)作出平面区域Ω(即三角区域ABC)如图所示,其中A(1,0),B(1,1),C(0,1).
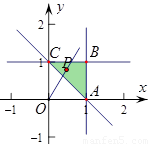
由图可得:0≤θ≤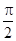 .
.
又f(θ)= sinθ+cosθ=2sin(θ+
sinθ+cosθ=2sin(θ+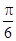 ),且
),且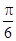 ≤θ+
≤θ+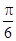 ≤
≤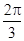 ,
,
故当θ+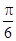 =
=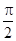 ,即θ=
,即θ=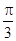 时,f(θ)取得最大值,且最大值等于2 ;
时,f(θ)取得最大值,且最大值等于2 ;
当θ+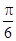 =
=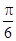 ,即θ=0时,f(θ)取得最小值,且最小值等于1.
,即θ=0时,f(θ)取得最小值,且最小值等于1.
考点:1、任意角三角函数的定义;2、二元不等式组表示的平面区域;3、三角函数的最值.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案科目:高中数学 来源:云南省祥云一中2010届高三第四次月考(数学理)尖子班 题型:044
已知向量![]() =(sinα,cosα),
=(sinα,cosα),![]() =(6sinα+cosα,7sinα-2cosα),设函数f(α)=
=(6sinα+cosα,7sinα-2cosα),设函数f(α)=![]() ·
·![]() .
.
(Ⅰ)求函数f(α)的最大值;
(Ⅱ)在锐角三角形ABC中,角A、B、C的对边分别为a、b、c,f(A)=6,且△ABC的面积为3,b+c=2+3![]() ,求A与a的值.
,求A与a的值.
查看答案和解析>>
科目:高中数学 来源:云南省祥云一中2010届高三第四次月考(数学理)普通班 题型:044
已知向量![]() =(sinα,cosα),
=(sinα,cosα),![]() =(6sinα+cosα,7sinα-2cosα),设函数f(α)=
=(6sinα+cosα,7sinα-2cosα),设函数f(α)=![]() ·
·![]() .
.
(Ⅰ)求函数f(α)的最大值;
(Ⅱ)在锐角三角形ABC中,角A、B、C的对边分别为a、b、c,f(A)=6,且△ABC的面积为3,b+c=2+3![]() ,求A与a的值.
,求A与a的值.
查看答案和解析>>
科目:高中数学 来源:湖南省长沙市一中2010届高三第一次模拟考试数学理科试题 题型:044
已知向量![]() =(8cosα,2),
=(8cosα,2),![]() =(sinα-cosα,3),设函数f(α)=
=(sinα-cosα,3),设函数f(α)=![]() .
.
(1)求函数f(α)的最大值;
(2)在锐角三角形ABC中,角A、B、C的对边分别为a、b、c,f(A)=6,且△ABC的面积为3,b+c=2+3![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数f(θ)=![]() sinθ+cosθ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
sinθ+cosθ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
(1)若点P的坐标为(![]() ,
,![]() ),求f(θ)的值;
),求f(θ)的值;
(2)若点P(x,y)为平面区域Ω: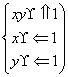 ,上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
,上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com