
【题目】定义在![]() 上的奇函数
上的奇函数![]() 有最小正周期
有最小正周期![]() ,且
,且![]() 时,
时,![]() .
.
(1)求![]() 在
在![]() 上的解析式;
上的解析式;
(2)判断![]() 在
在![]() 上的单调性,并给予证明;
上的单调性,并给予证明;
(3)当![]() 为何值时,关于方程
为何值时,关于方程![]() 在
在![]() 上有实数解?
上有实数解?
 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
【题目】(1)在![]() 中,内角A,B,C的对边分别为a,b,c,R表示
中,内角A,B,C的对边分别为a,b,c,R表示![]() 的外接圆半径.
的外接圆半径.
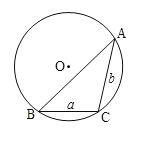
①如图,在以O圆心、半径为2的圆O中,![]() 和
和![]() 是圆O的弦,其中
是圆O的弦,其中![]() ,
,![]() ,求弦
,求弦![]() 的长;
的长;
②在![]() 中,若
中,若![]() 是钝角,求证:
是钝角,求证:![]() ;
;
(2)给定三个正实数a、b、R,其中![]() ,问:a、b、R满足怎样的关系时,以a、b为边长,R为外接圆半径的
,问:a、b、R满足怎样的关系时,以a、b为边长,R为外接圆半径的![]() 不存在、存在一个或存在两个(全等的三角形算作同一个)?在
不存在、存在一个或存在两个(全等的三角形算作同一个)?在![]() 存在的情况下,用a、b、R表示c.
存在的情况下,用a、b、R表示c.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程:在平面直角坐标系![]() 中,曲线
中,曲线![]() :
:![]() (
(![]() 为参数),在以平面直角坐标系的原点为极点、
为参数),在以平面直角坐标系的原点为极点、![]() 轴的正半轴为极轴,且与平面直角坐标系
轴的正半轴为极轴,且与平面直角坐标系![]() 取相同单位长度的极坐标系中,曲线
取相同单位长度的极坐标系中,曲线![]() :
:![]() .
.
(1)求曲线![]() 的普通方程以及曲线
的普通方程以及曲线![]() 的平面直角坐标方程;
的平面直角坐标方程;
(2)若曲线![]() 上恰好存在三个不同的点到曲线
上恰好存在三个不同的点到曲线![]() 的距离相等,求这三个点的极坐标.
的距离相等,求这三个点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为扩大教学规模,从今年起扩大招生,现有学生人数为![]() 人,以后学生人数年增长率为
人,以后学生人数年增长率为![]() .该校今年年初有旧实验设备
.该校今年年初有旧实验设备![]() 套,其中需要换掉的旧设备占了一半.学校决定每年以当年年初设备数量的
套,其中需要换掉的旧设备占了一半.学校决定每年以当年年初设备数量的![]() 的增长率增加新设备,同时每年淘汰
的增长率增加新设备,同时每年淘汰![]() 套旧设备.
套旧设备.
(1)如果10年后该校学生的人均占有设备的比率正好比目前翻一番,那么每年应更换的旧设备是多少套?
(2)依照(1)的更换速度,共需多少年能更换所有需要更换的旧设备?
下列数据提供计算时参考:
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某贫困地区共有1500户居民,其中平原地区1050户,山区450户.为调查该地区2017年家庭收入情况,从而更好地实施“精准扶贫”,采用分层抽样的方法,收集了150户家庭2017年年收入的样本数据(单位:万元).

(1)应收集多少户山区家庭的样本数据?
(2)根据这150个样本数据,得到2017年家庭收入的频率分布直方图(如图所示),其中样本数据分组区间为(0,0.5],(0.5,1],(1,1.5],(1.5,2],(2,2.5],(2.5,3].如果将频率视为概率,估计该地区2017年家庭收入超过1.5万元的概率;
(3)样本数据中,有5户山区家庭的年收入超过2万元,请完成2017年家庭收入与地区的列联表,并判断是否有90%的把握认为“该地区2017年家庭年收入与地区有关”?
超过2万元 | 不超过2万元 | 总计 | |
平原地区 | |||
山区 | 5 | ||
总计 |
附:
P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产的10件产品中,有8件合格品、2件不合格品,合格品与不合格品在外观上没有区别.从这10件产品中任意抽检2件,计算:
(1)抽出的2件产品恰好都是合格品的抽法有多少种?
(2)抽出的2件产品至多有1件不合格品的抽法有多少种?
(3)如果抽检的2件产品都是不合格品,那么这批产品将被退货,求这批产品被退货的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com