
【题目】已知抛物线![]() :
:![]() 和直线
和直线![]() :
:![]() ,
,![]() 是
是![]() 的焦点,
的焦点,![]() 是
是![]() 上一点,过
上一点,过![]() 作抛物线
作抛物线![]() 的一条切线与
的一条切线与![]() 轴交于
轴交于![]() ,则
,则![]() 外接圆面积的最小值为( )
外接圆面积的最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
设出过点P的切线方程,将切线方程与抛物线方程联立,即可得到切线斜率,进而得到点Q坐标,利用斜率乘积为-1可判断出![]() 为直角三角形,外接圆的圆心即为斜边的中点,即可求出圆的半径,从而得到圆的面积,即可得到最值.
为直角三角形,外接圆的圆心即为斜边的中点,即可求出圆的半径,从而得到圆的面积,即可得到最值.
将直线l与抛物线联立![]() ,得
,得![]() ,即直线l与抛物线相切且切点为(1,2),又
,即直线l与抛物线相切且切点为(1,2),又![]() 是
是![]() 上一点,
上一点,
当点P为切点(1,2)时,Q(0,1),F(1,0),此时![]() 为直角三角形,且外接圆的半径为1,故圆的面积为
为直角三角形,且外接圆的半径为1,故圆的面积为![]() ;
;
当点P不为切点时,设点![]() ,切线斜率为k,则切线方程为
,切线斜率为k,则切线方程为![]() ,即
,即![]() ,将切线方程与抛物线方程联立
,将切线方程与抛物线方程联立![]() 得
得![]() ,其中
,其中![]() ,则
,则![]() ,此时切线方程化简得
,此时切线方程化简得![]() ,此时点Q
,此时点Q![]() ,可得
,可得![]() ,即
,即![]() 为直角三角形,PF中点M
为直角三角形,PF中点M![]() 即为外接圆的圆心,则
即为外接圆的圆心,则![]() ,面积为
,面积为![]() ,当
,当![]() 时面积取到最小值为
时面积取到最小值为![]() ,
,
综上,面积最小值为![]() ,
,
故选:A.


科目:高中数学 来源: 题型:
【题目】如图1为某省2018年1~4月快递业务量统计图,图2是该省2018年1~4月快递业务收入统计图,下列对统计图理解错误的是( )


A. 2018年1~4月的业务量,3月最高,2月最低,差值接近2000万件
B. 2018年1~4月的业务量同比增长率均超过50%,在3月底最高
C. 从两图来看,2018年1~4月中的同一个月的快递业务量与收入的同比增长率并不完全一致
D. 从1~4月来看,该省在2018年快递业务收入同比增长率逐月增长
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以原点为极点,
为参数).以原点为极点,![]() 轴的非负半轴为极轴建立极坐标系,直线
轴的非负半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的极坐标方程;
的极坐标方程;
(2)若曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与
与![]() 在第一象限的交点为
在第一象限的交点为![]() ,与
,与![]() 的交点为
的交点为![]() (异于原点),求
(异于原点),求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《孙子算经》中有如下问题:“今有三女,长女五日一归,中女四日一归,少女三日一归.问:三女何日相会?”意思是:“一家出嫁的三个女儿中,大女儿每五天回一次娘家,二女儿每四天回一次娘家,小女儿每三天回一次娘家.三个女儿从娘家同一天走后,至少再隔多少天三人再次相会?”假如回娘家当天均回夫家,若当地风俗正月初二都要回娘家,则从正月初三算起的一百天内,有女儿回娘家的天数有( )
A.58B.59C.60D.61
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是正方体的平面展开图,在这个正方体中,正确的命题是( )

A. BD与CF成60°角 B. BD与EF成60°角 C. AB与CD成60°角 D. AB与EF成60°角
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国共产党第十九次全国代表大会于2017年10月18日至10月24日在北京召开,会议提出“决胜全面建成小康社会”.某市积极响应开展“脱贫攻坚”,为2020年“全面建成小康社会”贡献力量.为了解该市农村“脱贫攻坚”情况,从某县调查得到农村居民2013年至2017年家庭人均纯收入![]() (单位:百元)的数据如表:
(单位:百元)的数据如表:
年 份 | 2013 | 2014 | 2015 | 2016 | 2017 |
年人均纯收入 | 47 | 55 | 61 | 65 | 72 |
注:小康的标准是农村居民家庭年人均纯收入达到8000元.
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,预测2020年该县农村居民家庭年人均纯收入指标能否达到“全面建成小康社会”的标准?
附:回归直线![]() 斜率和截距的最小二乘估计公式分别为:
斜率和截距的最小二乘估计公式分别为:
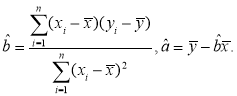
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线的顶点在原点,过点A(-4,4)且焦点在x轴.
(1)求抛物线方程;
(2)直线l过定点B(-1,0)与该抛物线相交所得弦长为8,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com