
【题目】在等差数列 ![]() 中,
中, ![]() ,其前
,其前 ![]() 项和为
项和为 ![]() ,等比数列
,等比数列 ![]() 的各项均为正数,
的各项均为正数, ![]() ,公比为
,公比为 ![]() ,且
,且 ![]() ,
, ![]() .
.
(Ⅰ)求 ![]() 与
与 ![]() .
.
(Ⅱ)设数列 ![]() 满足
满足 ![]() ,求
,求 ![]() 的前
的前 ![]() 项和
项和 ![]() .
.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某商场经营某种商品,在某周内获纯利![]() (元)与该周每天销售这种商品数
(元)与该周每天销售这种商品数![]() 之间的一组数据关系如表:
之间的一组数据关系如表:
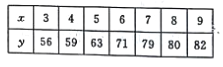
(I)画出散点图;
(II)求纯利![]() 与每天销售件数
与每天销售件数![]() 之间的回归直线方程;
之间的回归直线方程;
(III)估计当每天销售的件数为12件时,每周内获得的纯利为多少?
附注:
![]() ,
,![]() ,
,![]() ,
,![]() ,
, ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若平面点集 ![]() 满足:任意点
满足:任意点 ![]() ,存在
,存在 ![]() ,都有
,都有 ![]() ,则称该点集
,则称该点集 ![]() 是“
是“ ![]() 阶聚合”点集。现有四个命题:
阶聚合”点集。现有四个命题:
①若 ![]() ,则存在正数
,则存在正数 ![]() ,使得
,使得 ![]() 是“
是“ ![]() 阶聚合”点集;
阶聚合”点集;
②若 ![]() ,则
,则 ![]() 是“
是“ ![]() 阶聚合”点集;
阶聚合”点集;
③若 ![]() ,则
,则 ![]() 是“2阶聚合”点集;
是“2阶聚合”点集;
④若 ![]() 是“
是“ ![]() 阶聚合”点集,则
阶聚合”点集,则 ![]() 的取值范围是
的取值范围是 ![]() .
.
其中正确命题的序号为( )
A.①④
B.②③
C.①②
D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,点
,点![]() 在直线
在直线![]() 上.数列
上.数列![]() 满足
满足
![]()
![]() ,
,![]() ,且其前9项和为153.
,且其前9项和为153.
(Ⅰ)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(Ⅱ)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求使不等式
,求使不等式![]() 对一切
对一切![]() 都成立的最大正整数
都成立的最大正整数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题 ![]() “存在
“存在 ![]() ”,命题
”,命题 ![]() :“曲线
:“曲线 ![]() 表示焦点在
表示焦点在 ![]() 轴上的椭圆”,命题
轴上的椭圆”,命题 ![]() “曲线
“曲线 ![]() 表示双曲线”
表示双曲线”
(1)若“ ![]() 且
且 ![]() ”是真命题,求实数
”是真命题,求实数 ![]() 的取值范围;
的取值范围;
(2)若 ![]() 是
是 ![]() 的必要不充分条件,求实数
的必要不充分条件,求实数 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线 ![]() 的焦点为
的焦点为 ![]() ,其准线与
,其准线与 ![]() 轴交于点
轴交于点 ![]() ,过
,过 ![]() 作斜率为
作斜率为 ![]() 的直线
的直线 ![]() 与抛物线交于
与抛物线交于 ![]() 两点,弦
两点,弦 ![]() 的中点为
的中点为 ![]() 的垂直平分线与
的垂直平分线与 ![]() 轴交于
轴交于 ![]() .
.
(1)求 ![]() 的取值范围;
的取值范围;
(2)求证: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com