
【题目】已知函数 ![]() 函数
函数 ![]() ,其中
,其中 ![]() ,若函数
,若函数 ![]() 恰有4个零点,则
恰有4个零点,则 ![]() 的取值范围是 .
的取值范围是 .
【答案】![]()
【解析】∵ ![]() ,
,
∴ ![]() ,
,
∵函数y=f(x)g(x)恰好有四个零点,
∴方程f(x)g(x)=0有四个解,
即f(x)+f(2x)b=0有四个解,
即函数y=f(x)+f(2x)与y=b的图象有四个交点,
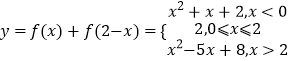 ,
,
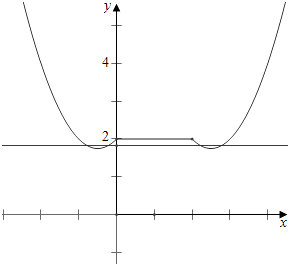
作函数y=f(x)+f(2x)与y=b的图象如下,
![]() ,
,
结合图象可知,
![]() <b<2,
<b<2,
所以答案是: ![]() .
.
【考点精析】认真审题,首先需要了解函数的零点与方程根的关系(二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点).


科目:高中数学 来源: 题型:
【题目】对于数集![]() ,其中
,其中![]() ,
, ![]() .定义向量集
.定义向量集![]() .若对于任意
.若对于任意![]() ,存在
,存在![]() ,使得
,使得![]() ,则称
,则称![]() 具有性质
具有性质![]() .例如
.例如![]() 具有性质
具有性质![]() .
.
(1)若![]() ,且
,且![]() 具有性质
具有性质![]() ,求
,求![]() 的值;
的值;
(2)若![]() 具有性质
具有性质![]() ,求证:
,求证: ![]() ,且当
,且当![]() 时,
时, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的首项a1=a(a>0),其前n项和为Sn , 设bn=an+an+1(n∈N*).
(1)若a2=a+1,a3=2a2 , 且数列{bn}是公差为3的等差数列,求S2n;
(2)设数列{bn}的前n项和为Tn , 满足Tn=n2 .
①求数列{an}的通项公式;
②若对n∈N*,且n≥2,不等式(an﹣1)(an+1-1)≥2(1﹣n)恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}及fn(x)=a1x+a2x2+…+anxn , fn(﹣1)=(﹣1)nn,n=1,2,3,…
(1)求a1 , a2 , a3的值;
(2)求数列{an}的通项公式;
(3)求证: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com