
【题目】某校为创建“绿色校园”,在校园内种植树木,有A、B、C三种树木可供选择,已知这三种树木6年内的生长规律如下:
A树木:种植前树木高0.84米,第一年能长高0.1米,以后每年比上一年多长高0.2米;
B树木:种植前树木高0.84米,第一年能长高0.04米,以后每年生长的高度是上一年生长高度的2倍;
C树木:树木的高度![]() (单位:米)与生长年限
(单位:米)与生长年限![]() (单位:年,
(单位:年,![]() )满足如下函数:
)满足如下函数:![]() (
(![]() 表示种植前树木的高度,取
表示种植前树木的高度,取![]() ).
).
(1)若要求6年内树木的高度超过5米,你会选择哪种树木?为什么?
(2)若选C树木,从种植起的6年内,第几年内生长最快?
【答案】(1)选择C;(2)第4或第5年.
【解析】
(1)根据已知求出三种树木六年末的高度,判断得解;(2)设![]() 为第
为第![]() 年内树木生长的高度,先求出
年内树木生长的高度,先求出![]() ,设
,设![]() ,则
,则![]() ,
,![]() .再利用分析函数的单调性,分析函数的图像得解.
.再利用分析函数的单调性,分析函数的图像得解.
(1)由题意可知,A、B、C三种树木随着时间的增加,高度也在增加,
6年末:A树木的高度为![]() (米):
(米):
B树木的高度为![]() (米):
(米):
C树木的高度为![]() (米),
(米),
所以选择C树木.
(2)设![]() 为第
为第![]() 年内树木生长的高度,
年内树木生长的高度,
则![]() ,
,
所以![]() ,
,![]() ,
,![]() .
.
设![]() ,则
,则![]() ,
,![]() .
.
令![]() ,因为
,因为![]() 在区间
在区间![]() 上是减函数,在区间
上是减函数,在区间![]() 上是增函数,
上是增函数,
所以当![]() 时,
时,![]() 取得最小值,从而
取得最小值,从而![]() 取得最大值,此时
取得最大值,此时![]() ,解得
,解得![]() ,
,
因为![]() ,
,![]() ,故
,故![]() 的可能值为3或4,
的可能值为3或4,
又![]() ,
,![]() ,即
,即![]() .
.
因此,种植后第4或第5年内该树木生长最快.


科目:高中数学 来源: 题型:
【题目】土笋冻是闽南种广受欢迎的特色传统风味小吃某小区超市销售一款土笋冻,进价为每个15元,售价为每个20元.销售的方案是当天进货,当天销售,未售出的全部由厂家以每个10元的价格回购处理.根据该小区以往的销售情况,得到如图所示的频率分布直方图:

(1)估算该小区土笋冻日需求量的平均数![]() (同一组中的数据用该组区间的中点值代表);
(同一组中的数据用该组区间的中点值代表);
(2)已知该超市某天购进了150个土笋冻,假设当天的需求量为![]() 个
个![]() 销售利润为
销售利润为![]() 元.
元.
(i)求关于![]() 的函数关系式;
的函数关系式;
(ii)结合上述频率分布直方图,以额率估计概率的思想,估计当天利润![]() 不小于650元的概率.
不小于650元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2018年高校自主招生期间,某校把学生的平时成绩按“百分制”折算,选出前![]() 名学生,并对这
名学生,并对这![]() 名学生按成绩分组,第一组
名学生按成绩分组,第一组![]() ,第二组
,第二组![]() ,第三组
,第三组![]() ,第四组
,第四组![]() ,第五组
,第五组![]() .如图为频率分布直方图的一部分,其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列,且第四组的人数为60.
.如图为频率分布直方图的一部分,其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列,且第四组的人数为60.
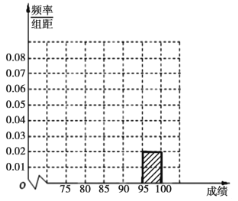
(1)请写出第一、二、三、五组的人数,并在图中补全频率分布直方图;
(2)若![]() 大学决定在成绩高的第3,4,5组中用分层抽样的方法抽取6名学生进行面试.
大学决定在成绩高的第3,4,5组中用分层抽样的方法抽取6名学生进行面试.
①若![]() 大学本次面试中有
大学本次面试中有![]() ,
,![]() ,
,![]() 三位考官,规定获得至少两位考官的认可即为面试成功,且各考官面试结果相互独立.已知甲同学已经被抽中,并且通过这三位考官面试的概率依次为
三位考官,规定获得至少两位考官的认可即为面试成功,且各考官面试结果相互独立.已知甲同学已经被抽中,并且通过这三位考官面试的概率依次为![]() ,
,![]() ,
,![]() ,求甲同学面试成功的概率;
,求甲同学面试成功的概率;
②若![]() 大学决定在这6名学生中随机抽取3名学生接受考官
大学决定在这6名学生中随机抽取3名学生接受考官![]() 的面试,第3组有
的面试,第3组有![]() 名学生被考官
名学生被考官![]() 面试,求
面试,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市地铁全线共有四个车站,甲、乙两人同时在地铁第1号车站(首发站)乘车,假设每人自第2号站开始,在每个车站下车是等可能的,约定用有序实数对![]() 表示“甲在
表示“甲在![]() 号车站下车,乙在
号车站下车,乙在![]() 号车站下车”
号车站下车”
(Ⅰ)用有序实数对把甲、乙两人下车的所有可能的结果列举出来;
(Ⅱ)求甲、乙两人同在第3号车站下车的概率;
(Ⅲ)求甲、乙两人在不同的车站下车的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为
的焦距为![]() ,且过点
,且过点![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() 为椭圆
为椭圆![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() .取点
.取点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 轴于点
轴于点![]() .点
.点![]() 是点
是点![]() 关于
关于![]() 轴的对称点,作直线
轴的对称点,作直线![]() ,问这样作出的直线
,问这样作出的直线![]() 是否与椭圆
是否与椭圆![]() 一定有唯一的公共点?并说明理由.
一定有唯一的公共点?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com