
设椭圆![]() 过点
过点![]() ,且左焦点为
,且左焦点为![]()
(Ⅰ)求椭圆C的方程;
(Ⅱ)当过点P(4,1)的动直线l与椭圆C相交于两不同点A,B时,在线段AB上取点Q,满足![]() 。证明:点Q总在某定直线上。
。证明:点Q总在某定直线上。
解:(Ⅰ)由题意:
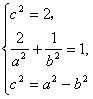 解得:
解得:![]()
所求的椭圆方程为 ![]()
(Ⅱ) 方法一:
设点Q、A、B的坐标分别为(x, y)、(![]() )、(
)、(![]() )
)
由题设知![]() 均不为零,记
均不为零,记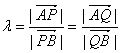 ,
,
则![]() 。
。
又 A,P,B,Q四点共线,从而![]()
于是![]() ,
,![]() ,
,![]() ,
, ![]()
从而![]() ,…①;
,…①;![]() …②
…②
又点A,B在椭圆C上,即![]() …③;
…③;![]() …④
…④
①+2![]() 并结合③、④得:4x+2y=4,即点Q(x, y)总在定直线2x+y-2=0上。
并结合③、④得:4x+2y=4,即点Q(x, y)总在定直线2x+y-2=0上。
方法二:
设点Q、A、B的坐标分别为(x, y)、(![]() )、(
)、(![]() )
)
由题设知![]() 均不为零,,
均不为零,,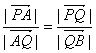
又 A,P,B,Q四点共线,可设![]() ,于是
,于是
![]() ,
,![]() ,…①;
,…①;![]() ,
,![]() …②
…②
由于A(![]() ),B(
),B(![]() )在椭圆C上,将①、②分别代入C的方程
)在椭圆C上,将①、②分别代入C的方程![]() ,整理得:
,整理得:
![]() …③
…③
![]() …④
…④
④-③得:8(2x+y-2)=0,∵![]() ,∴
,∴![]()
即点Q(x, y)总在定直线2x+y-2=0上。


科目:高中数学 来源:2008年普通高等学校招生全国统一考试(安徽卷)、数学(理)试卷与答案详解 题型:044
设椭圆![]() 过点
过点![]() ,且左焦点为
,且左焦点为![]()
(Ⅰ)求椭圆C的方程;
(Ⅱ)当过点P(4,1)的动直线l与椭圆C相交于两不同点A,B时,在线段AB上取点Q,满足![]() .证明:点Q总在某定直线上.
.证明:点Q总在某定直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年安徽卷理) (本小题满分13分)
设椭圆![]() 过点
过点![]() ,且左焦点为
,且左焦点为![]()
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)当过点![]() 的动直线
的动直线![]() 与椭圆
与椭圆![]() 相交于两不同点
相交于两不同点![]() 时,在线段
时,在线段![]() 上取点
上取点![]() ,满足
,满足![]() 。证明:点Q总在某定直线上。
。证明:点Q总在某定直线上。
查看答案和解析>>
科目:高中数学 来源:2010年广东省高考数学考点预测:解析几何(解析版) 题型:解答题
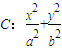 =1(a>b>0)过点
=1(a>b>0)过点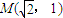 ,且左焦点为
,且左焦点为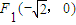
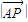 •
•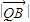 =
=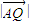 •
•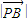 ,证明:点Q总在某定直线上.
,证明:点Q总在某定直线上.查看答案和解析>>
科目:高中数学 来源:2008年安徽省高考数学试卷(理科)(解析版) 题型:解答题
 =1(a>b>0)过点
=1(a>b>0)过点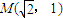 ,且左焦点为
,且左焦点为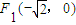
 •
•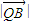 =
=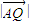 •
•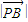 ,证明:点Q总在某定直线上.
,证明:点Q总在某定直线上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com