
分析 (1)由题意可求A,T,利用周期公式可求ω,利用f(x)=3sin(2x+φ)过点($\frac{π}{3}$,3),可求φ的值,解得函数解析式,利用正弦函数的单调性即可计算得解f(x)的单调递增区间.
(2)利用函数y=Asin(ωx+φ)的图象变换规律可得函数g(x)的解析式,进而利用正弦函数的图象和性质可求其值域.
解答 解:(1)∵最高点的坐标为($\frac{π}{3}$,3),可得:3=Asin($\frac{π}{3}$ω+φ)≤A,可得:A=3,
∵图象的一个最高点的坐标为($\frac{π}{3}$,3),且当x1+x2=$\frac{7π}{6}$时,满足f(x1)=-f(x2).
∴图象的一个最低点的坐标为($\frac{5π}{6}$,-3),
∴当函数f(x)的周期最大时,周期T=2($\frac{5π}{6}$-$\frac{π}{3}$)=π=$\frac{2π}{ω}$,解得:ω=2,
∵f(x)=3sin(2x+φ)过点($\frac{π}{3}$,3),
∴可得:$\frac{2π}{3}$+φ=$\frac{π}{2}$,解得:φ=-$\frac{π}{6}$,
∴f(x)=3sin(2x-$\frac{π}{6}$).
∴令2kπ-$\frac{π}{2}$≤2x-$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,k∈Z,解得:kπ-$\frac{π}{6}$≤x≤kπ+$\frac{π}{3}$,k∈Z,
∴f(x)的单调递增区间为:[kπ-$\frac{π}{6}$,kπ+$\frac{π}{3}$],k∈Z.
(2)将函数f(x)=3sin(2x-$\frac{π}{6}$)的图象上每个点的横坐标缩短为原来的$\frac{1}{2}$倍,纵坐标不变,
可得函数解析式为:y=3sin(4x-$\frac{π}{6}$),
再将所得函数图象向左平移$\frac{π}{12}$得到函数g(x)的图象,
可得函数解析式为:g(x)=3sin[4(x+$\frac{π}{12}$)-$\frac{π}{6}$]=3sin(4x+$\frac{π}{6}$),
∵x∈[$\frac{π}{24}$,$\frac{7π}{24}$],
∴4x+$\frac{π}{6}$∈[$\frac{π}{3}$,$\frac{4π}{3}$],可得:sin(4x+$\frac{π}{6}$)∈[-$\frac{\sqrt{3}}{2}$,1],g(x)=3sin(4x+$\frac{π}{6}$)∈[-$\frac{3\sqrt{3}}{2}$,3],
可得:函数g(x)在[$\frac{π}{24}$,$\frac{7π}{24}$]上的值域为:[-$\frac{3\sqrt{3}}{2}$,3].
点评 本题着重考查了三角恒等变换、三角函数的图象与性质、函数值域的求法以及函数y=Asin(ωx+φ)的图象变换等知识,属于中档题.


科目:高中数学 来源: 题型:填空题
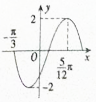 函数f(x)=2sin(ωx+φ$)(ω>0,-\frac{π}{2}<$(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则f(x)的图象可由函数g(x)=2sinωx的图象至少向右平移$\frac{π}{6}$个单位得到.
函数f(x)=2sin(ωx+φ$)(ω>0,-\frac{π}{2}<$(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则f(x)的图象可由函数g(x)=2sinωx的图象至少向右平移$\frac{π}{6}$个单位得到.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<$\frac{1}{2}$} | B. | {x|x<0或0<x<$\frac{1}{2}$} | C. | {x|x>$\frac{1}{2}$} | D. | {x|0<x<$\frac{1}{2}$} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
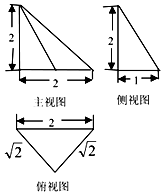
| A. | $\frac{1}{3}$ | B. | 1 | C. | $\frac{4}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 参加书法班 | 未参加书法班 | |
| 参加演讲班 | 8 | 5 |
| 未参加演讲班 | 2 | 33 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com