
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线
),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若极坐标为![]() 的点
的点![]() 在曲线C1上,求曲线C1与曲线C2的交点坐标;
在曲线C1上,求曲线C1与曲线C2的交点坐标;
(2)若点![]() 的坐标为
的坐标为![]() ,且曲线C1与曲线C2交于
,且曲线C1与曲线C2交于![]() 两点,求|PB||PD|
两点,求|PB||PD|
【答案】(1)![]() (2)6
(2)6
【解析】分析:(1)点![]() 对应的直角坐标为(1,1),由曲线C1的参数方程知:曲线C1是过点(﹣1,3)的直线,利用点斜式可得曲线C1的方程.曲线C2的极坐标方程即
对应的直角坐标为(1,1),由曲线C1的参数方程知:曲线C1是过点(﹣1,3)的直线,利用点斜式可得曲线C1的方程.曲线C2的极坐标方程即![]() ,展开后,利用互化公式即可得出曲线C2的直角坐标方程联立即可得出交点坐标.
,展开后,利用互化公式即可得出曲线C2的直角坐标方程联立即可得出交点坐标.
(2)由直线参数方程可判断知:P在直线C1上,将参数方程代入圆的方程得:t2﹣4(cosα﹣sinα)t+6=0,设点B,D对应的参数分别为t1,t2,利用|PB||PD|=|t1||t2|=|t1t2|即可得出.
详解:(1)点![]() 对应的直角坐标为
对应的直角坐标为![]() ,
,
由曲线![]() 的参数方程知:曲线
的参数方程知:曲线![]() 是过点
是过点![]() 的直线,故曲线
的直线,故曲线![]() 的方程为
的方程为![]() ,
,
而曲线![]() :
:![]() 展开得:
展开得:![]()
得直角坐标方程为![]() ,
,
联立得![]() ,解得:
,解得:![]() ,
,
故交点坐标分别为![]()
(2)由判断知:![]() 在直线
在直线![]() 上,将
上,将![]() 代入方程
代入方程![]() 得:
得:
![]() ,设点
,设点![]() 对应的参数分别为
对应的参数分别为![]() ,
,
则![]() ,而
,而![]() ,
,
所以![]()


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:
【题目】设函数![]() 是定义在
是定义在![]() 上的函数,①若存在
上的函数,①若存在![]() ,使得
,使得![]() 成立,则函数
成立,则函数![]() 在
在![]() 上单调递增。②若存在
上单调递增。②若存在![]() ,使得
,使得![]() 成立,则函数在
成立,则函数在![]() 上不可能单调递减. ③若存在
上不可能单调递减. ③若存在![]() 对于任意
对于任意![]() 都有
都有![]() 成立,则函数在
成立,则函数在![]() 上递增。④对于任意的
上递增。④对于任意的![]() ,都有
,都有![]() 成立,则函数在
成立,则函数在![]() 上单调递减。
上单调递减。
则以上真命题的个数为( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了保护学生的视力,课桌和椅子的高度都是按一定的关系配套设计的,研究表明:假设课桌的高度为![]() ,椅子的高度为
,椅子的高度为![]() ,则y应是x的一次函数,下表列出两套符合条件的课桌和椅子的高度:
,则y应是x的一次函数,下表列出两套符合条件的课桌和椅子的高度:
第一套 | 第二套 | |
椅子高度 | 40.0 | 37.0 |
课桌高度 | 75.0 | 70.2 |
(1)请你确定y与x的函数关系式(不必写出x的取值范围);
(2)现有一把高42.0 cm的椅子和一张高78.2cm的课桌,它们是否配套?为什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD–A1B1C1D1中,已知底面ABCD是菱形,点P是侧棱C1C的中点.

(1)求证:AC1∥平面PBD;
(2)求证:BD⊥A1P.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在《周易》中,长横“ ”表示阳爻,两个短横“ ”表示阴爻,有放回地取阳爻和阴爻三次合成一卦,共有![]() 种组合方法,这便是《系辞传》所说:“太极生两仪,两仪生四象,四象生八卦”,有放回地取阳爻和阴爻一次有2种不同的情况,有放回地取阳爻和阴爻两次有四种不同的情况,有放回地取阳爻和阴爻三次有八种不同的情况,即为八卦,在一次卜卦中,恰好出现两个阳爻一个阴爻的概率是( )
种组合方法,这便是《系辞传》所说:“太极生两仪,两仪生四象,四象生八卦”,有放回地取阳爻和阴爻一次有2种不同的情况,有放回地取阳爻和阴爻两次有四种不同的情况,有放回地取阳爻和阴爻三次有八种不同的情况,即为八卦,在一次卜卦中,恰好出现两个阳爻一个阴爻的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图、![]() 后从事互联网行业者岗位分布条形图,则下列结论中不一定正确的是( )
后从事互联网行业者岗位分布条形图,则下列结论中不一定正确的是( )
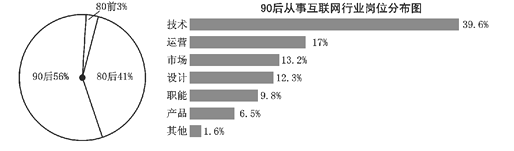
A. 互联网行业从业人员中![]() 后占一半以上
后占一半以上
B. 互联网行业中从事技术岗位的人数超过总人数的![]()
C. 互联网行业中从事运营岗位的人数![]() 后比
后比![]() 前多
前多
D. 互联网行业中从事运营岗位的人数![]() 后比
后比![]() 后多
后多
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com