
【题目】定义在R上的奇函数![]() ,当
,当![]() 时,
时, 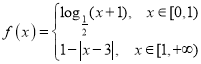
则函数![]() 的所有零点之和为_____.
的所有零点之和为_____.
【答案】![]()
【解析】
函数F(x)=f(x)﹣a(0<a<1)的零点转化为:在同一坐标系内y=f(x),y=a的图象交点的横坐标;作出两函数图象,考查交点个数,结合方程思想,及零点的对称性,根据奇函数f(x)在x≥0时的解析式,作出函数的图象,结合图象及其对称性,求出答案.
∵当x≥0时,
f(x)=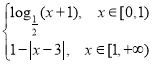
即x∈[0,1)时,f(x)=![]() (x+1)∈(﹣1,0];
(x+1)∈(﹣1,0];
x∈[1,3]时,f(x)=x﹣2∈[﹣1,1];
x∈(3,+∞)时,f(x)=4﹣x∈(﹣∞,﹣1);
画出x≥0时f(x)的图象,
再利用奇函数的对称性,画出x<0时f(x)的图象,如图所示;
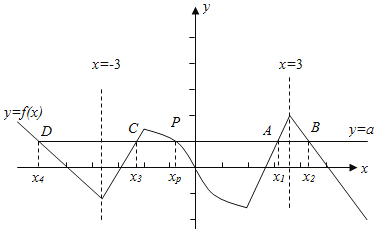
则直线y=a,与y=f(x)的图象有5个交点,则方程f(x)﹣a=0共有五个实根,
最左边两根之和为﹣6,最右边两根之和为6,
∵x∈(﹣1,0)时,﹣x∈(0,1),
∴f(﹣x)=![]() (﹣x+1),
(﹣x+1),
又f(﹣x)=﹣f(x),
∴f(x)=﹣![]() (﹣x+1)=
(﹣x+1)=![]() (1﹣x)﹣1=log2(1﹣x),
(1﹣x)﹣1=log2(1﹣x),
∴中间的一个根满足log2(1﹣x)=a,即1﹣x=2a,
解得x=1﹣2a,
∴所有根的和为1﹣2a.
故答案为:1﹣2a.


科目:高中数学 来源: 题型:
【题目】从某企业的某种产品中抽取![]() 件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:
件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:
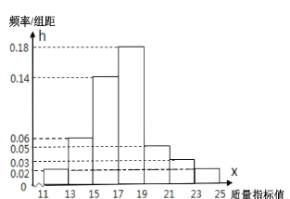
(Ⅰ)求这![]() 件产品质量指标值的样本平均数
件产品质量指标值的样本平均数![]() 和样本方差
和样本方差![]() (同一组数据用该区间的中点值作代表,记作
(同一组数据用该区间的中点值作代表,记作![]() ,
,![]() );
);
(Ⅱ)由频率分布直方图可以认为,这种产品的质量指标值![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(i)若使![]() 的产品的质量指标值高于企业制定的合格标准,则合格标准的质量指标值大约为多少?
的产品的质量指标值高于企业制定的合格标准,则合格标准的质量指标值大约为多少?
(ii)若该企业又生产了这种产品![]() 件,且每件产品相互独立,则这
件,且每件产品相互独立,则这![]() 件产品质量指标值不低于
件产品质量指标值不低于![]() 的件数最有可能是多少?
的件数最有可能是多少?
附:参考数据与公式:![]() ,
,![]() ;若
;若![]() ,则①
,则①![]() ;②
;②![]() ;③
;③![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小学对五年级的学生进行体质测试,已知五年一班共有学生30人,测试立定跳远的成绩用茎叶图表示如图(单位:![]() ):男生成绩在175
):男生成绩在175![]() 以上(包括175
以上(包括175![]() )定义为“合格”,成绩在175
)定义为“合格”,成绩在175![]() 以下(不包括175
以下(不包括175![]() )定义为“不合格”.女生成绩在165
)定义为“不合格”.女生成绩在165![]() 以上(包括165
以上(包括165![]() )定义为“合格”,成绩在165
)定义为“合格”,成绩在165![]() 以下(不包括165
以下(不包括165![]() )定义为“不合格”.
)定义为“不合格”.
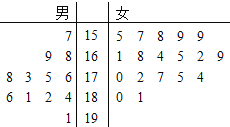
(1)求五年一班的女生立定跳远成绩的中位数;
(2)在五年一班的男生中任意选取3人,求至少有2人的成绩是合格的概率;
(3)若从五年一班成绩“合格”的学生中选取2人参加复试,用![]() 表示其中男生的人数,写出
表示其中男生的人数,写出![]() 的分布列,并求
的分布列,并求![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数,
为常数,![]() 且
且![]() ),且数列
),且数列![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列.
的等差数列.
(1)求证:数列![]() 是等比数列;
是等比数列;
(2)若![]() ,当
,当![]() 时,求数列
时,求数列![]() 的前
的前![]() 项和
项和![]() 的最小值;
的最小值;
(3)若![]() ,问是否存在实数
,问是否存在实数![]() ,使得
,使得![]() 是递增数列?若存在,求出
是递增数列?若存在,求出![]() 的范围;若不存在,说明理由.
的范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市计划在一片空地上建一个集购物、餐饮、娱乐为一体的大型综合园区,如图,已知两个购物广场的占地都呈正方形,它们的面积分别为13公顷和8公顷;美食城和欢乐大世界的占地也都呈正方形,分别记它们的面积为![]() 公顷和
公顷和![]() 公顷;由购物广场、美食城和欢乐大世界围成的两块公共绿地都呈三角形,分别记它们的面积为
公顷;由购物广场、美食城和欢乐大世界围成的两块公共绿地都呈三角形,分别记它们的面积为![]() 公顷和
公顷和![]() 公顷.
公顷.
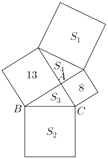
(1)设![]() ,用关于
,用关于![]() 的函数
的函数![]() 表示
表示![]() ,并求
,并求![]() 在区间
在区间![]() 上的最大值的近似值(精确到0.001公顷);
上的最大值的近似值(精确到0.001公顷);
(2)如果![]() ,并且
,并且![]() ,试分别求出
,试分别求出![]() 、
、![]() 、
、![]() 、
、![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于实数![]() ,将满足“
,将满足“![]() 且
且![]() 为整数”的实数
为整数”的实数![]() 称为实数
称为实数![]() 的小数部分,用记号
的小数部分,用记号![]() 表示.对于实数
表示.对于实数![]() ,无穷数列
,无穷数列![]() 满足如下条件:
满足如下条件:![]() ,
,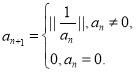 其中
其中![]() .
.
(1)若![]() ,求数列
,求数列![]() ;
;
(2)当![]() 时,对任意的
时,对任意的![]() ,都有
,都有![]() ,求符合要求的实数
,求符合要求的实数![]() 构成的集合
构成的集合![]() ;
;
(3)若![]() 是有理数,设
是有理数,设![]() (
(![]() 是整数,
是整数,![]() 是正整数,
是正整数,![]() 互质),问对于大于
互质),问对于大于![]() 的任意正整数
的任意正整数![]() ,是否都有
,是否都有![]() 成立,并证明你的结论.
成立,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知无穷数列![]() 的前n项和为
的前n项和为![]() ,记
,记![]() ,
, ![]() ,…,
,…, ![]() 中奇数的个数为
中奇数的个数为![]() .
.
(Ⅰ)若![]() = n,请写出数列
= n,请写出数列![]() 的前5项;
的前5项;
(Ⅱ)求证:"![]() 为奇数,
为奇数, ![]() (i = 2,3,4,...)为偶数”是“数列
(i = 2,3,4,...)为偶数”是“数列![]() 是单调递增数列”的充分不必要条件;
是单调递增数列”的充分不必要条件;
(Ⅲ)若![]() ,i=1, 2, 3,…,求数列
,i=1, 2, 3,…,求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某温室大棚规定,一天中,从中午12点到第二天上午8点为保温时段,其余4小时为工作作业时段,从中午12点连续测量20小时,得出此温室大棚的温度y(单位:度)与时间t(单位:小时,![]() )近似地满足函数
)近似地满足函数![]() 关系,其中,b为大棚内一天中保温时段的通风量。
关系,其中,b为大棚内一天中保温时段的通风量。
(1)若一天中保温时段的通风量保持100个单位不变,求大棚一天中保温时段的最低温度(精确到0.1℃);
(2)若要保持一天中保温时段的最低温度不小于17℃,求大棚一天中保温时段通风量的最小值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com