
【题目】对于函数![]() ,若存在定义域
,若存在定义域![]() 内某个区间
内某个区间![]() ,使得
,使得![]() 在
在![]() 上的值域也是
上的值域也是![]() ,则称函数
,则称函数![]() 在定义域
在定义域![]() 上封闭.如果函数
上封闭.如果函数![]() 在
在![]() 上封闭,那么实数
上封闭,那么实数![]() 的取值范围是______.
的取值范围是______.
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源: 题型:
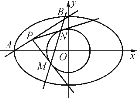
【题目】已知椭圆C:![]() =1(a>b>0),点A、B分别是椭圆C的左顶点和上顶点,直线AB与圆G:x2+y2=
=1(a>b>0),点A、B分别是椭圆C的左顶点和上顶点,直线AB与圆G:x2+y2=![]() (c是椭圆的半焦距)相离,P是直线AB上一动点,过点P作圆G的两切线,切点分别为M、N.
(c是椭圆的半焦距)相离,P是直线AB上一动点,过点P作圆G的两切线,切点分别为M、N.
(1)若椭圆C经过两点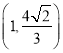 、
、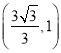 ,求椭圆C的方程;
,求椭圆C的方程;
(2)当c为定值时,求证:直线MN经过一定点E,并求![]() ·
·![]() 的值(O是坐标原点);
的值(O是坐标原点);
(3)若存在点P使得△PMN为正三角形,试求椭圆离心率的取值范围..
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,椭圆E :![]() 的焦距为4,两条准线间的距离为8,A,B分别为椭圆E的左、右顶点.
的焦距为4,两条准线间的距离为8,A,B分别为椭圆E的左、右顶点.

(1)求椭圆E 的标准方程;
(2)已知图中四边形ABCD 是矩形,且BC=4,点M,N分别在边BC,CD上,AM与BN相交于第一象限内的点P .①若M,N分别是BC,CD的中点,证明:点P在椭圆E上;②若点P在椭圆E上,证明:![]() 为定值,并求出该定值.
为定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,AB=4,AD=2,E是CD的中点,将△ADE沿AE折起,得到如图2所示的四棱锥D1—ABCE,其中平面D1AE⊥平面ABCE.
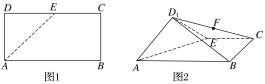
(1)证明:BE⊥平面D1AE;
(2)设F为CD1的中点,在线段AB上是否存在一点M,使得MF∥平面D1AE,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设复数![]() ,其中xnyn∈R,n∈N*,i为虚数单位,
,其中xnyn∈R,n∈N*,i为虚数单位,![]() ,z1=3+4i,复数zn在复平面上对应的点为Zn.
,z1=3+4i,复数zn在复平面上对应的点为Zn.
(1)求复数z2,z3,z4的值;
(2)是否存在正整数n使得![]() ?若存在,求出所有满足条件的
?若存在,求出所有满足条件的![]() ;若不存在,请说明理由;
;若不存在,请说明理由;
(3)求数列![]() 的前
的前![]() 项之和.
项之和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①,有一个长方体形状的敞口玻璃容器,底面是边长为20cm的正方形,高为30cm,内有20cm深的溶液.现将此容器倾斜一定角度![]() (图②),且倾斜时底面的一条棱始终在桌面上(图①、②均为容器的纵截面).
(图②),且倾斜时底面的一条棱始终在桌面上(图①、②均为容器的纵截面).
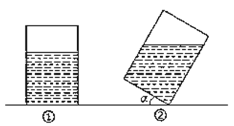
(1)要使倾斜后容器内的溶液不会溢出,角![]() 的最大值是多少?
的最大值是多少?
(2)现需要倒出不少于![]() 的溶液,当
的溶液,当![]() 时,能实现要求吗?请说明理由.
时,能实现要求吗?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设椭圆![]() 两顶点
两顶点![]() ,短轴长为4,焦距为2,过点
,短轴长为4,焦距为2,过点![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 两点.设直线
两点.设直线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
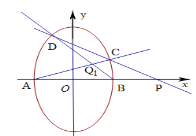
(1)求椭圆的方程;
(2)求线段![]() 中点
中点![]() 的轨迹方程;
的轨迹方程;
(3)求证:点![]() 的横坐标为定值.
的横坐标为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“总把新桃换旧符”(王安石)、“灯前小草写桃符”(陆游),春节是中华民族的传统节日,在宋代人们用写“桃符”的方式来祈福避祸,而现代人们通过贴“福”字、贴春联、挂灯笼等方式来表达对新年的美好祝愿,某商家在春节前开展商品促销活动,顾客凡购物金额满50元,则可以从“福”字、春联和灯笼这三类礼品中任意免费领取一件,若有4名顾客都领取一件礼品,则他们中有且仅有2人领取的礼品种类相同的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com