
分析 (1)由题知,可设 f(x)=ax2+bx+4,方程f(x)=2x有两实数根:x1=1,x2=4,求得a,b的值,可得函数的解析式.
(2)由于h(x)=(x-t)2+4-t2,其对称轴为x=t.分①当t≤0时、②当0<t<1时、③当t≥1时三种情况,分别根据最小值是$\frac{7}{2}$,求出t的值.
(3)根据新定义,将f(x)=x2-3x+4与g(x)=2x+m在[0,3]上是“关联函数”,转化为函数y=x2-5x+4-m在[0,3]上有两个不同的零点即可.
解答 解:(1)∵二次函数f(x)的图象过点(0,4),
设二次函数为f(x)=ax2+bx+4,
∵f(x)=2x有两实数根:x1=1,x2=4,
∴ax2+(b-2)x+4=0.的根为x1=1,x2=4,
∴1+4=-$\frac{b-2}{a}$,1×4=$\frac{4}{a}$,
∴a=1,b=-3,
∴f(x)=x2-3x+4;
(2)h(x)=f(x)-(2t-3)x=x2-2tx+4=(x-t)2+4-t2,其对称轴为x=t.
①当t≤0时,函数在[0,1]上单调递增,h(x)min=h(0)=4≠$\frac{7}{2}$,
②当0<t<1时,h(x)在[0,t]上单调递减,在[t,1]上单调递增,
h(x)min=h(t)=4-t2=$\frac{7}{2}$,解得t=$\frac{\sqrt{2}}{2}$,t=-$\frac{\sqrt{2}}{2}$(舍去),
③当t≥1时,函数在[0,1]上单调递减,h(x)min=h(1)=5-2t=$\frac{7}{2}$,解得t=$\frac{3}{4}$(舍去)
综上所述,t的值为$\frac{\sqrt{2}}{2}$;
(3)若函数f(x)=x2-3x+4与g(x)=2x+m在[0,3]上是“Ω函数”,
则函数F(x)=f(x)-g(x)=x2-5x+4-m在[0,3]上有两个不同的零点,
再根据二次函数F(x)的图象的对称轴为x=$\frac{5}{2}$,则 $\left\{\begin{array}{l}{△=(-5)^{2}-4(4-m)>0}\\{F(0)=0-0+4-m≥0}\\{F(3)=9-15+4-m≥0}\end{array}\right.$,解得-$\frac{9}{4}$<m≤-2,
即m的范围为:(-$\frac{9}{4}$,-2].
点评 本题主要考查用待定系数法求函数的解析式,求二次函数在闭区间上的最值,函数的零点的定义和求法,属于中档题.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{6}}{3}$ | C. | $\frac{2\sqrt{3}}{3}$或2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
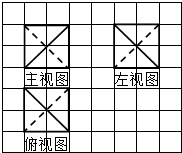
| A. | $\frac{2\sqrt{3}}{9π}$ | B. | $\frac{\sqrt{3}}{9π}$ | C. | $\frac{\sqrt{2}}{16π}$ | D. | $\frac{8\sqrt{2}}{π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3$\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com