
如图,已知抛物线 的焦点为
的焦点为 ,过焦点
,过焦点 且不平行于
且不平行于 轴的动直线
轴的动直线 交抛物线于
交抛物线于 ,
, 两点,抛物线在
两点,抛物线在 、
、 两点处的切线交于点
两点处的切线交于点 .
.
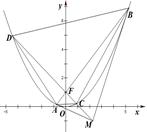
(Ⅰ)求证: ,
, ,
, 三点的横坐标成等差数列;
三点的横坐标成等差数列;
(Ⅱ)设直线 交该抛物线于
交该抛物线于 ,
, 两点,求四边形
两点,求四边形 面积的最小值.
面积的最小值.
(Ⅰ)可设直线 的方程
的方程 (
( ),
), ,
, ,由
,由 消去
消去 ,得
,得 ,
, .
.  ,
, ,由
,由 ,得
,得 ,所以
,所以 ,直线
,直线 的斜率为
的斜率为 直线
直线 的方程为
的方程为  同理,直线
同理,直线 的方程为
的方程为  M的横坐标
M的横坐标 即
即 ,
, ,
, 三点的横坐标成等差数列(Ⅱ)32
三点的横坐标成等差数列(Ⅱ)32
【解析】
试题分析:(Ⅰ)由已知,得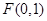 ,显然直线
,显然直线 的斜率存在且不为0,则可设直线
的斜率存在且不为0,则可设直线 的方程
的方程
 (
( ),
), ,
, ,
,

由 消去
消去 ,得
,得 ,
,
 .
.  ,
, 2分
2分
由 ,得
,得 ,所以
,所以 ,直线
,直线 的斜率为
的斜率为 ,
,
所以,直线 的方程为
的方程为 ,又
,又 ,
,
所以,直线 的方程为
的方程为  ①
4分
①
4分
同理,直线 的方程为
的方程为  ②
5分
②
5分
②-①并据 得点M的横坐标
得点M的横坐标 ,
,
即 ,
, ,
, 三点的横坐标成等差数列
7分
三点的横坐标成等差数列
7分
(Ⅱ)由①②易得y=-1,所以点M的坐标为(2k,-1)( ).
).
所以 ,则直线MF的方程为
,则直线MF的方程为 8分
8分
设C(x3,y3),D(x4,y4),
由 消去
消去 ,得
,得 ,
,

 ,
, . 9分
. 9分
又
 10分
10分

 12分
12分
因为 ,所以
,所以 ,
,
所以, ,
,
当且仅当 时,四边形
时,四边形 面积的取到最小值
面积的取到最小值 14分
14分
考点:抛物线方程及直线与抛物线的相交的位置关系弦长等
点评:当直线与圆锥曲线相交时,常联立方程组转化为关于x的二次方程,进而利用方程的根与系数的关系设而不求的方法化简,在求解时弦长公式 经常用到,本题中函数在某一点的切线问题要借助于导数的几何意义求出切线斜率
经常用到,本题中函数在某一点的切线问题要借助于导数的几何意义求出切线斜率


科目:高中数学 来源:2014届江苏省高三10月质量检测理科数学试卷(解析版) 题型:解答题
如图,已知抛物线 的焦点为F
的焦点为F 过点
过点 的直线交抛物线于A
的直线交抛物线于A ,B
,B 两点,直线AF,BF分别与抛物线交于点M,N
两点,直线AF,BF分别与抛物线交于点M,N

(1)求 的值;
的值;
(2)记直线MN的斜率为 ,直线AB的斜率为
,直线AB的斜率为 证明:
证明: 为定值
为定值
查看答案和解析>>
科目:高中数学 来源:2012-2013学年辽宁省高三第五次模拟理数试卷(解析版) 题型:解答题
(本小题满分12分)
如图,已知抛物线 的焦点为
的焦点为 .过点
.过点 的直线交抛物线于
的直线交抛物线于 ,
, 两点,直线
两点,直线 ,
, 分别与抛物线交于点
分别与抛物线交于点 ,
, .
.

(Ⅰ)求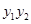 的值;
的值;
(Ⅱ)记直线 的斜率为
的斜率为 ,直线
,直线 的斜率为
的斜率为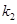 .证明:
.证明: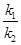 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省盐城市高三摸底考试数学卷 题型:解答题
(本小题满分16分)
如图,已知抛物线 的焦点为
的焦点为 ,
, 是抛物线上横坐标为8且位于
是抛物线上横坐标为8且位于 轴上方的点.
轴上方的点.  到抛物线准线的距离等于10,过
到抛物线准线的距离等于10,过 作
作 垂直于
垂直于 轴,垂足为
轴,垂足为 ,
, 的中点为
的中点为 (
( 为坐标原点).
为坐标原点).
(Ⅰ)求抛物线 的方程;
的方程;
(Ⅱ)过 作
作 ,垂足为
,垂足为 ,求点
,求点 的坐标;
的坐标;
(Ⅲ)以 为圆心,4为半径作圆
为圆心,4为半径作圆 ,点
,点 是
是 轴上的一个动点,试讨论直线
轴上的一个动点,试讨论直线 与圆
与圆 的位置关系.
的位置关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com