练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在平面直角坐标系中，直线的参数方程为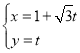（为参数），以坐标原点为极点，轴的非负半轴为极轴建立极坐标系，圆的极坐标方程为.

    （1）求圆的圆心到直线的距离；

    （2）已知，若直线与圆交于两点，为的中点，求的值.

    【答案】（1）；（2）

    【解析】

    （1）消参后直接得到直线的普通方程，以及根据，写圆的直角坐标方程，再求圆心到直线的距离；（2）将直线的参数方程写成，与圆的方程联立，得到，，，根据的几何意义表示距离求解.

    （1）直线的普通方程是：

    由圆的极坐标方程可知，即，

    那么圆的标准方程是，圆心,

    则圆心到直线的距离；

    （2）直线的斜率是，则倾斜角是，则，，

    则直线的参数方程写成 （为参数），直线与圆的方程联立，可得

    ，，

    所以都是负数，

    是的中点，所以，

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】由甲乙两位同学组成一个小组参加年级组织的篮球投篮比赛，共进行两轮投篮，每轮甲乙各自独立投篮一次，并且相互不受影响，每次投中得2分，没投中得0分.已知甲同学每次投中的概率为，乙同学每次投中的概率为

    （1）求第一轮投篮时，甲乙两位同学中至少有一人投中的概率；

    （2）甲乙两位同学在两轮投篮中，记总得分为随机变量ξ，求ξ的分布列和期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直角中，，，，、分别是、上一点，且满足平分，，以为折痕将折起，使点到达点的位置，且平面平面.

    （1）证明：；

    （2）求二面角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率，焦距为2，直线与椭圆交于，两点.

    （1）求椭圆的标准方程；

    （2）若直线过椭圆的右焦点，且，求直线方程；

    （3）设为坐标原点，直线，的斜率分别为，，若，求面积的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义在上的函数若满足：①对任意、，都有；②对任意，都有，则称函数为“中心捺函数”，其中点称为函数的中心.已知函数是以为中心的“中心捺函数”，若满足不等式，当时，的取值范围为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】高斯是德国著名的数学家，近代数学奠基者之一，享有“数学王子”的称号，用其名字命名的“高斯函数”为：设，用表示不超过的最大整数，则称为高斯函数，例如：，．已知函数，函数，则下列命题中真命题的个数是（ ）

    ①图象关于对称；

    ②是奇函数；

    ③在上是增函数；

    ④的值域是.

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知曲线C的极坐标方程是，以极点为原点，极轴为x轴的正半轴建立平面直角坐标系，曲线C经过伸缩变换得到曲线E，直线（t为参数）与曲线E交于A，B两点．

    （1）设曲线C上任一点为，求的最小值；

    （2）求出曲线E的直角坐标方程，并求出直线l被曲线E截得的弦AB长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，若方程恰有5个不同的实数根，则实数a的取值范围________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某部门在上班高峰时段对甲、乙两座地铁站各随机抽取了50名乘客，统计其乘车等待时间（指乘客从进站口到乘上车的时间，单位：分钟）将统计数据按，，，…，分组，制成频率分布直方图如图所示：

    （1）求a的值；

    （2）记A表示事件“在上班高峰时段某乘客在甲站乘车等待时间少于20分钟”试估计A的概率；

    （3）假设同组中的每个数据用该组区间左端点值来估计，记在上班高峰时段甲、乙两站各抽取的50名乘客乘车的平均等待时间分别为，求的值，并直接写出与的大小关系.

    查看答案和解析>>

    同步练习册答案