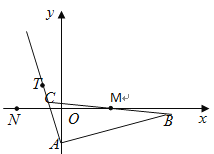
[题目]已知抛物线C:y2=2px和动直线l:y=kx+b(k.b是参变量.且k≠0．b≠0)相交于A(x1 . y2).N)x2 . y2)两点.直角坐标系原点为O.记直线OA.OB的斜率分别为kOAkOB= 恒成立.则当k变化时直线l恒经过的定点为( )A.(﹣ p.0)B.(﹣2 p.0)C.(﹣ .0)D.(﹣ .0) 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知抛物线C：y2=2px（p＞0）和动直线l：y=kx+b（k，b是参变量，且k≠0．b≠0）相交于A（x1 ， y2），N）x2 ， y2）两点，直角坐标系原点为O，记直线OA，OB的斜率分别为kOAkOB= 恒成立，则当k变化时直线l恒经过的定点为（）
A.（﹣ p，0）
B.（﹣2 p，0）
C.（﹣ ，0）
D.（﹣ ，0）

【答案】D
【解析】解：将直线与抛物线联立，消去y，得k2x2+（2kb﹣2p）x+b2=0， ∴x1+x2= ，x1x2= ；
∵kOAkOB= ，∴y1y2= x1x2 ，
∴y1y2=（kx1+b）（kx2+b）
=k2x1x2+kb（x1+x2）+b2
= ；
∴ = ，
解得b= ，
∴y=kx+ =k（x+ ）
令x=﹣ ，得y=0，
∴直线过定点（﹣ ，0）．
故选D．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知向量，，函数．
（1）求函数f（x）的单调递增区间；
（2）已知a，b，c分别为△ABC内角A，B，C的对边，其中A为锐角，，c=1，且f（A）=1，求△ABC的面积S．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】现有1000根某品种的棉花纤维，从中随机抽取50根，纤维长度（单位：mm）的数据分组及各组的频数如表，据此估计这1000根中纤维长度不小于37.5mm的根数是．

纤维长度	频数
[22.5，25.5）	3
[25.5，28.5）	8
[28.5，31.5）	9
[31.5，34.5）	11
[34.5，37.5）	10
[37.5，40.5）	5
[40.5，43.5]	4

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设函数，则关于函数f（x）有以下四个命题（）
①x∈R，f（f（x））=1；
②x0 ， y0∈R，f（x0+y0）=f（x0）+f（y0）；
③函数f（x）是偶函数；
④函数f（x）是周期函数．
其中真命题的个数是（）
A.4
B.3
C.2
D.1

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知椭圆的离心率为，四个顶点构成的菱形的面积是4，圆M：（x+1）2+y2=r2（0＜r＜1）．过椭圆C的上顶点A作圆M的两条切线分别与椭圆C相交于B，D两点（不同于点A），直线AB，AD的斜率分别为k1 ， k2 ．
（1）求椭圆C的方程；
（2）当r变化时，①求k1k2的值；②试问直线BD是否过某个定点？若是，求出该定点；若不是，请说明理由．