
【题目】如图,平面![]() 平面
平面![]() ,其中
,其中![]() 为矩形,
为矩形,![]() 为直角三角形,
为直角三角形,![]() ,
,![]() .
.
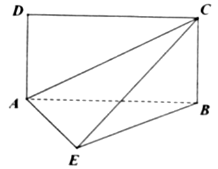
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)运用线面垂直的判定定理及面面垂直的判定定理推证;(2)运用线面角的定义运用解直角三角形的方法求解或建立空间直角坐标系,运用空间向量的数量积求解.
试题解析:
(1)∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]()
![]()
![]() ,
,![]() 平面
平面![]()
∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
∴![]()
又![]() ,
,![]()
∴![]() 平面
平面![]()
而![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
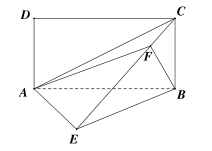
(2)解法一:
∵![]()
∴![]() 与平面
与平面![]() 所成角的大小等于
所成角的大小等于![]() 与平面
与平面![]() 所成角的大小
所成角的大小
过![]() 作
作![]() 于
于![]() ,连接
,连接![]()
∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴![]() 平面
平面![]()
∴![]() 即为
即为![]() 与平面
与平面![]() 所成的角
所成的角
由![]() ,得
,得![]() ,
,![]()
∴![]()
∴直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
解法二:以![]() 为原点,
为原点,![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,
,
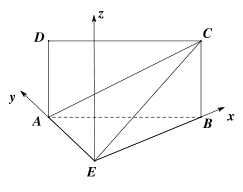
则![]()
于是,![]() ,
,![]() ,
,![]()
设![]() 为平面
为平面![]() 的法向量
的法向量
由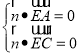 得
得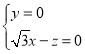
取![]()
设![]() 与
与![]() 的夹角为
的夹角为![]()
所以![]()
所以![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() .
.


 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:
【题目】A,B两城相距100 km,在两地之间距A城x km处的D地建一核电站给A,B两城供电.为保证城市安全,核电站与城市距离不得少于10 km.已知供电费用与供电距离的平方和供电量之积成正比,比例系数λ=0.25.若A城供电量为20亿度/月,B城为10亿度/月.
(1)求x的取值范围;
(2)把月供电总费用y表示成x的函数;
(3)核电站建在距A城多远,才能使供电费用最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国的烟火名目繁多,花色品种繁杂.其中“菊花”烟花是最壮观的烟花之一,制造时一般是期望在它达到最高点时爆裂,通过研究,发现该型烟花爆裂时距地面的高度![]() (单位:米)与时间
(单位:米)与时间![]() (单位:秒)存在函数关系,并得到相关数据如下表:
(单位:秒)存在函数关系,并得到相关数据如下表:

(1)根据上表数据,从下列函数中,选取一个函数描述该型烟花爆裂时距地面的高度![]() 与时间
与时间![]() 的变化关系:
的变化关系:![]() ,确定此函数解析式,并简单说明理由;
,确定此函数解析式,并简单说明理由;
(2)利用你选取的函数,判断烟花爆裂的最佳时刻,并求出此时烟花距地面的高度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用反证法证明“a,b,c中至少有一个大于0”,下列假设正确的是()
A. 假设a,b,c都小于0 B. 假设a,b,c都大于0
C. 假设a,b,c中都不大于0 D. 假设a,b,c中至多有一个大于0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点(-3,-1)和(4,-6)在直线3x-2y-a=0的两侧,则实数a的取值范围为( )
A. (-7,24)
B. (-∞,-7)∪(24,+∞)
C. (-24,7)
D. (-∞,-24)∪(7,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥P﹣ABCD中,四边形ABCD为正方形,PD⊥平面ABCD,PD=DA=2,F,E分别为AD、PC的中点.
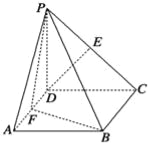
(1)证明:DE∥平面PFB;
(2)求三棱锥A﹣PFB的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用反证法证明命题“等腰三角形的底角必是锐角”,下列假设正确的是( )
A. 等腰三角形的顶角不是锐角 B. 等腰三角形的底角为直角
C. 等腰三角形的底角为钝角 D. 等腰三角形的底角为直角或钝角
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com