【题目】已知函数
，在点M（1，f（1））处的切线方程为9x+3y-10=0，求
（1）实数a，b的值；
（2）函数f（x）的单调区间以及在区间[0，3]上的最值．
【答案】（1）
；（2）见解析
【解析】
求出曲线的斜率，切点坐标，求出函数的导数，利用导函数值域斜率的关系，即可求出
的值
求出导函数的符号，判断函数的单调性以及求解区间上的函数的最值
（1）因为在点M（1，f（1））处的切线方程为9x+3y-10=0，
所以切线斜率是k=-3且9×1+3f（1）-10=0，
求得
，即点
又函数
，则f′（x）=x2-a
所以依题意得
-
解得
（2）由（1）知
所以f′（x）=x2-4=（x+2）（x-2）
令f′（x）=0，解得x=2或x=-2
当f′（x）＞0x＞2或x＜-2；当f′（x）＜0-2＜x＜2
所以函数f（x）的单调递增区间是（-∞，-2），（2，+∞）
单调递减区间是（-2，2）
又x∈[0，3]
所以当x变化时，f（x）和f′（x）变化情况如下表：
X | 0 | （0，2） | 2 | （2，3） | 3 |
f′（x） | - | 0 | + | 0 | |
f（x） | 4 | ↘ | 极小值 | ↗ | 1 |
所以当x∈[0，3]时，f（x）max=f（0）=4，
-
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】已知数列{an}是等差数列，Sn为{an}的前n项和，且a10=19，S10=100；数列{bn}对任意n∈N* ， 总有b1b2b3…bn﹣1bn=an+2成立．
（Ⅰ）求数列{an}和{bn}的通项公式；
（Ⅱ）记cn=（﹣1）n 
，求数列{cn}的前n项和Tn ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，⊙O是以AB为直径的圆，点C在圆上，在△ABC和△ACD中，∠ADC=90°，∠BAC=∠CAD，DC的延长线与AB的延长线交于点E．若EB=6，EC=6 
，则BC的长为 ．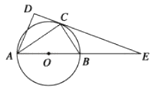 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了解学生寒假阅读名著的情况，一名教师对某班级的所有学生进行了调查，调查结果如下表：
本数 | 0 | 1 | 2 | 3 | 4 | 5 |
男生 | 0 | 1 | 4 | 3 | 2 | 2 |
女生 | 0 | 0 | 1 | 3 | 3 | 1 |
（I）从这班学生中任选一名男生，一名女生，求这两名学生阅读名著本数之和为4的概率；
（II）若从阅读名著不少于4本的学生中任选4人，设选到的男学生人数为 X，求随机变量 X的分布列和数学期望；
（III）试判断男学生阅读名著本数的方差 
与女学生阅读名著本数的方差 
的大小（只需写出结论）．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
：
（
）的右焦点为
，且椭圆
上一点
到其两焦点
，
的距离之和为
．
（1）求椭圆
的标准方程；
（2）设直线
：
（
）与椭圆
交于不同两点
，
，且
，若点
满足
，求
的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在斜三棱柱ABC﹣A1B1C1中，底面ABC是正三角形，E是AB中点，A1E⊥平面ABC．
（I）证明：BC1∥平面 A1EC；
（II）若A1A⊥A1B，且AB=2．
①求点B到平面ACC1A1的距离；
②求直线CB1与平面ACC1A1所成角的正弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】以平面直角坐标系原点O为极点，以x轴非负半轴为极轴，以平面直角坐标系的长度单位为长度单位建立极坐标系．已知直线l的参数方程为 
（t为参数），曲线C的极坐标方程为ρsin2θ=4cosθ
（Ⅰ） 求曲线C的直角坐标方程；
（Ⅱ） 设直线l与曲线C相交于A，B两点，求|AB|．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
