
【题目】已知函数![]() (其中
(其中![]() 为自然对数的底数)
为自然对数的底数)
(1)求![]() 的单调区间;
的单调区间;
(2)已知关于![]() 的方程
的方程![]() 有三个实根,求实数
有三个实根,求实数![]() 的取值范围.
的取值范围.
【答案】(1)单调递增区间为![]() 和
和![]() ,无单调递减区间;(2)
,无单调递减区间;(2)![]() .
.
【解析】
(1)求出函数![]() 的定义域和导数,利用导数可求出函数
的定义域和导数,利用导数可求出函数![]() 的单调区间;
的单调区间;
(2)由题意可知,关于![]() 的方程
的方程![]() 在
在![]() 时有三个根,令
时有三个根,令![]() ,利用导数分析函数
,利用导数分析函数![]() 的单调性与极值,利用数形结合思想,结合内层函数与外层函数的零点,对实数
的单调性与极值,利用数形结合思想,结合内层函数与外层函数的零点,对实数![]() 的取值进行分类讨论,分析方程
的取值进行分类讨论,分析方程![]() 的实根个数,从而可得出实数
的实根个数,从而可得出实数![]() 的取值范围.
的取值范围.
(1)函数![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
所以,函数![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,无单调递减区间;
,无单调递减区间;
(2)由![]() ,得
,得![]() ,得
,得![]() .
.
令![]() ,则
,则![]() ,令
,令![]() ,得
,得![]() ,列表如下:
,列表如下:
|
|
|
|
|
|
|
|
|
|
|
| 极小值 |
|
|
如下图所示,当![]() 时,方程
时,方程![]() 在
在![]() 时有两根,当
时有两根,当![]() 或
或![]() 时,方程
时,方程![]() 在
在![]() 时只有一根.
时只有一根.

作出函数![]() 与函数
与函数![]() 的图象如下图所示:
的图象如下图所示:

①当![]() 时,直线
时,直线![]() 与函数
与函数![]() 图象交点的横坐标为
图象交点的横坐标为![]() ,
,
此时方程![]() 在
在![]() 时只有一根,不合乎题意;
时只有一根,不合乎题意;
②当![]() 时,直线
时,直线![]() 与函数
与函数![]() 图象有两个交点,横坐标分别为
图象有两个交点,横坐标分别为![]() 、
、![]() ,且
,且![]() ,
,![]() ,
,
方程![]() 在
在![]() 时只有一根,方程
时只有一根,方程![]() 在
在![]() 时只有一根,共有两根,不合乎题意;
时只有一根,共有两根,不合乎题意;
③当![]() 时,直线
时,直线![]() 与函数
与函数![]() 图象交点的横坐标为
图象交点的横坐标为![]() ,
,
方程![]() 只有一根,不合乎题意;
只有一根,不合乎题意;
④当![]() 时,直线
时,直线![]() 与函数
与函数![]() 图象有两个交点,横坐标分别为
图象有两个交点,横坐标分别为![]() 、
、![]() ,且
,且![]() ,
,![]() ,
,
方程![]() 在
在![]() 时有两根,方程
时有两根,方程![]() 在
在![]() 时只有一根,共有三根,合乎题意;
时只有一根,共有三根,合乎题意;
⑤当![]() 时,直线
时,直线![]() 与函数
与函数![]() 图象交点的横坐标为
图象交点的横坐标为![]() ,
,![]() ,
,
方程![]() 在
在![]() 时有一根,方程
时有一根,方程![]() 在
在![]() 时也只有一根,共两根,不合乎题意;
时也只有一根,共两根,不合乎题意;
⑥当![]() 时,直线
时,直线![]() 与函数
与函数![]() 图象交点的横坐标为
图象交点的横坐标为![]() ,且
,且![]() ,
,
此时,方程![]() 在
在![]() 时只有一根,不合乎题意.
时只有一根,不合乎题意.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,D,E分别为AB,AC的中点,O为DE的中点,AB=AC=2![]() ,BC=4.将△ADE沿DE折起到△A1DE的位置,使得平面A1DE
,BC=4.将△ADE沿DE折起到△A1DE的位置,使得平面A1DE![]() 平面BCED,如下图.
平面BCED,如下图.

(Ⅰ)求证:A1O![]() BD;
BD;
(Ⅱ)求直线A1C和平面A1BD所成角的正弦值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机构为了了解不同年龄的人对一款智能家电的评价,随机选取了50名购买该家电的消费者,让他们根据实际使用体验进行评分.
(Ⅰ)设消费者的年龄为![]() ,对该款智能家电的评分为
,对该款智能家电的评分为![]() .若根据统计数据,用最小二乘法得到
.若根据统计数据,用最小二乘法得到![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() ,且年龄
,且年龄![]() 的方差为
的方差为![]() ,评分
,评分![]() 的方差为
的方差为![]() .求
.求![]() 与
与![]() 的相关系数
的相关系数![]() ,并据此判断对该款智能家电的评分与年龄的相关性强弱.
,并据此判断对该款智能家电的评分与年龄的相关性强弱.
(Ⅱ)按照一定的标准,将50名消费者的年龄划分为“青年”和“中老年”,评分划分为“好评”和“差评”,整理得到如下数据,请判断是否有![]() 的把握认为对该智能家电的评价与年龄有关.
的把握认为对该智能家电的评价与年龄有关.
好评 | 差评 | |
青年 | 8 | 16 |
中老年 | 20 | 6 |
附:线性回归直线![]() 的斜率
的斜率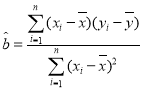 ;相关系数
;相关系数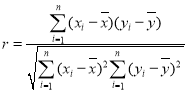 ,独立性检验中的
,独立性检验中的![]() ,其中
,其中![]() .
.
临界值表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,设
,设![]() .
.
(1)若![]() ,记数列
,记数列![]() 的前
的前![]() 项和为
项和为![]() .①求证:数列
.①求证:数列![]() 为等差数列;②若不等式
为等差数列;②若不等式![]() 对任意的
对任意的![]() 都成立,求实数
都成立,求实数![]() 的最小值;
的最小值;
(2)若![]() ,且
,且![]() ,是否存在正整数
,是否存在正整数![]() ,使得无穷数列
,使得无穷数列![]() ,
,![]() ,
,![]() ,…成公差不为0的等差数列?若存在,给出数列
,…成公差不为0的等差数列?若存在,给出数列![]() 的一个通项公式;若不存在,请说明理由.
的一个通项公式;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“搜索指数”是网民通过搜索引擎,以每天搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大,表示网民对该关键词的搜索次数越多,对该关键词相关的信息关注度也越高.下图是2017年9月到2018年2月这半年中,某个关键词的搜索指数变化的走势图.

根据该走势图,下列结论正确的是( )
A. 这半年中,网民对该关键词相关的信息关注度呈周期性变化
B. 这半年中,网民对该关键词相关的信息关注度不断减弱
C. 从网民对该关键词的搜索指数来看,去年10月份的方差小于11月份的方差
D. 从网民对该关键词的搜索指数来看,去年12月份的平均值大于今年1月份的平均值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】劳动教育是中国特色社会主义教育制度的重要内容,某高中计划组织学生参与各项职业体验,让学生在劳动课程中掌握一定劳动技能,理解劳动创造价值,培养劳动自立意识和主动服务他人、服务社会的情怀.学校计划下周在高一年级开设“缝纫体验课”,聘请“织补匠人”李阿姨给同学们传授织补技艺。高一年级有6个班,李阿姨每周一到周五只有下午第2节课的时间可以给同学们上课,所以必须安排有两个班合班上课,高一年级6个班“缝纫体验课”的不同上课顺序有( )
A.600种B.3600种C.1200种D.1800种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在平行四边形ABCD中,![]() ,
,![]() ,
,![]() ,点E是CD边的中点,将
,点E是CD边的中点,将![]() 沿AE折起,使点D到达点P的位置,且
沿AE折起,使点D到达点P的位置,且![]() .
.

(1)求证;平面![]() 平面ABCE;
平面ABCE;
(2)求点E到平面PAB的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1所示,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 中点,将
中点,将![]() 沿
沿![]() 折起,使点
折起,使点![]() 到点
到点![]() 处,且平面
处,且平面![]() 平面
平面![]() ,如图2所示.
,如图2所示.
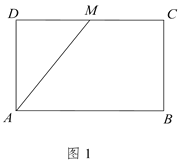
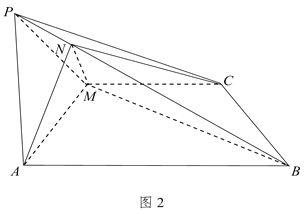
(1)求证:![]() :
:
(2)在棱![]() 上取点
上取点![]() ,使平面
,使平面![]() 平面
平面![]() ,求平面
,求平面![]() 与
与![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com