
����Ŀ��ijѧУ�о���ѧϰС��Ը�У����ѧ������������е��飬�ڸ�����ȫ��1000��ѧ���������ȡ��100��ѧ�������������õ���ͼ��Ƶ�ʷֲ�ֱ��ͼ.
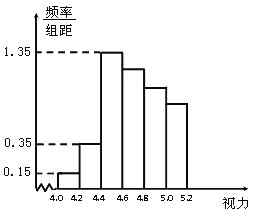

��1����ֱ��ͼ�к������Ƶ���ɵȲ����У��Թ���ȫ�꼶������5.0���µ�������
��2��ѧϰС���Ա���֣�ѧϰ�ɼ�ͻ����ѧ�������ӵıȽ϶࣬Ϊ���о�ѧ����������ѧϰ�ɼ��Ƿ��й�ϵ�����꼶������1��50����951��1000����ѧ�������˵��飬�õ��ұ������ݣ����ݱ��е����ݣ��ܷ��ڷ����ĸ��ʲ�����0.05��ǰ������Ϊ������ѧϰ�ɼ��й�ϵ?
��3���ڣ�2���е����100��ѧ���У����շֲ�����ڲ����ӵ�ѧ���г�ȡ��9�ˣ���һ�������������õĻ���ϰ�ߣ���������9������ȡ3�ˣ���������1��50��ѧ������Ϊ![]() ����
����![]() �ķֲ��к���ѧ����.
�ķֲ��к���ѧ����.
����

![]()
���𰸡���1��820�ˣ���2���ڷ�����ĸ��ʲ�����0.05��ǰ������Ϊ������ѧϰ�ɼ��й�ϵ����3���ֲ��м�����������Ϊ1��
�������������������������Ƶ�ʷֲ�ֱ��ͼ��֪����ǰ�����Ƶ�ʳɵȱ����У��������Ƶ�ʳɵȲ�����ʱ��![]() ���µ�Ƶ��Ϊ
���µ�Ƶ��Ϊ![]() ����ȫ�꼶������
����ȫ�꼶������![]() ���µ�����ԼΪ
���µ�����ԼΪ![]() ��
��
��������![]() ������ڷ�����ĸ��ʲ�����
������ڷ�����ĸ��ʲ�����![]() ��ǰ������Ϊ������ѧϰ�ɼ��й�ϵ��
��ǰ������Ϊ������ѧϰ�ɼ��й�ϵ��
����������![]() ��ȡ
��ȡ![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
����![]() ����ѧ����
����ѧ����![]() .
.
���������������������Ƶ��Ϊ![]() ��
��
�����⣬ǰ�����Ƶ�ʳɵȱ����У��������Ƶ�ʳɵȲ����У���
![]() ��
��![]() ��
��![]()
������![]() ��
��![]() ��
��
����������5.0���µ�Ƶ��Ϊ1-0.17=0.83��
��ȫ�꼶������5.0���µ�����ԼΪ![]()
(��)![]()
����ڷ�����ĸ��ʲ�����0.05��ǰ������Ϊ������ѧϰ�ɼ��й�ϵ.
������������9�����꼶������1��50����951��1000���ֱ���3�˺�6�ˣ�
![]() ��ȡ0��1��2��3��
��ȡ0��1��2��3��
![]() ��
��![]() ��
��
![]() ��
��![]()
![]() �ķֲ���Ϊ
�ķֲ���Ϊ
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
![]() ����ѧ����
����ѧ����![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��C��D����ABΪֱ����Բ�����㣬AB=2AD=2![]() ��AC=BC��F ��AB��һ�㣬��AF=
��AC=BC��F ��AB��һ�㣬��AF=![]() AB����Բ��ֱ��AB����ʹ��C��ƽ��ABD����ӰE��BD�ϣ���֪CE=
AB����Բ��ֱ��AB����ʹ��C��ƽ��ABD����ӰE��BD�ϣ���֪CE=![]() ��
��

��1����֤��AD��ƽ��BCE��
��2����֤��AD��ƽ��CEF��
��3��������A��CFD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��д����������ķ����ж������������٣�
��1�����κ���![]() ��ͼ��Ķ���������
��ͼ��Ķ���������![]() ��
��
��2������������������������
��3������һ�������ڽ�С��60���������Σ�
��4��������ʵ��t����![]() ����һ�κ���
����һ�κ���![]() ��ͼ���ϣ�
��ͼ���ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�
�У�![]() ƽ��
ƽ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��

����֤����![]() ƽ��
ƽ��![]() ��
��
�������߶�![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() �������ڣ���
�������ڣ���![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧһλ���������ζԱ���50��ѧ��ѧϰ�����ԺͶԴ��༶������̬�Ƚ��е��飬�õ���ͳ�����������ʾ��
�����μӰ༶���� | �������μӰ༶���� | �ϼ� | |
ѧϰ�����Ը� | 18 | 7 | 25 |
ѧϰ�����Բ��� | 6 | 19 | 25 |
�ϼ� | 24 | 26 | 50 |
��1������������������һ��ѧ������ô�鵽�������μӰ༶������ѧϰ�����Բ��ߵ�ѧ���ĸ����Ƕ��٣�
��2�����������μӰ༶������ѧϰ�����Ըߵ�7��ѧ�����������������ִ��г�ȡ2��ѧ���μ�ij������2��ѧ������1�������ĸ����Ƕ��٣�
��3��ѧ����ѧϰ��������Դ��༶������̬���Ƿ��й�ϵ����˵�����ɣ�
����

![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �Ľ���Ϊ
�Ľ���Ϊ![]() ����Ϊ
����Ϊ![]() ��
��![]() ���������ϵ��������㣬������
���������ϵ��������㣬������![]() �����߶�
�����߶�![]() ���е�
���е�![]() ��
��![]() �ϵ�ͶӰΪ
�ϵ�ͶӰΪ![]() ����
����![]() �����ֵ��_______.
�����ֵ��_______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ں���![]() �������ĸ����ۣ�������ȷ�Ľ����ǣ� ��
�������ĸ����ۣ�������ȷ�Ľ����ǣ� ��
A.f(x)��ż����B.f(x)�����䣨![]() ,
,![]() ����������
����������
C.f(x)��![]() ��4�����D.f(x)�����ֵΪ2
��4�����D.f(x)�����ֵΪ2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() ��������
��������![]() ����������,�е�ֱ�Ϊ
����������,�е�ֱ�Ϊ![]() ,
,![]() ,
,![]() ,
,![]() �ֱ�
�ֱ�![]() ����
����![]() ,
,![]() ����,
����,![]() Ϊ����ԭ��,��
Ϊ����ԭ��,��![]() ��
��![]() �����֮��Ϊ( )
�����֮��Ϊ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com