已知函数y=f(x)是定义在R上的奇函数,且当x≥0时,f(x)=-x2+ax.
(1)当a=-2时,求函数f(x)的解析式;
(2)若函数f(x)为单调递减函数;
①直接写出a的范围(不必证明);
②若对任意实数m,f(m-1)+f(m2+t)<0恒成立,求实数t的取值范围.
解:(1)当x<0时,-x>0,又因为f(x)为奇函数,
所以f(x)=-f(-x)=-(-x
2+2x)=x
2-2x,
所以f(x)=
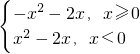
.
(2)①当a≤0时,对称轴
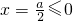
,所以f(x)=-x
2+ax在[0,+∞)上单调递减,
由于奇函数关于原点对称的区间上单调性相同,所以f(x)在(-∞,0)上单调递减,
所以a≤0时,f(x)在R上为单调递减函数,
当a>0时,f(x)在(0,

)递增,在(

,+∞)上递减,不合题意,
所以函数f(x)为单调减函数时,a的范围为a≤0.
②f(m-1)+f(m
2+t)<0,∴f(m-1)<-f(m
2+t),
又f(x)是奇函数,∴f(m-1)<f(-t-m
2),
又因为f(x)为R上的单调递减函数,所以m-1>-t-m
2恒成立,
所以
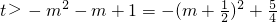
恒成立,所以
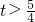
.
即实数t的范围为:(

,+∞).
分析:(1)当x<0时,-x>0,由已知表达式可求f(-x),根据奇函数性质可求f(x);
(2)①借助二次函数图象的特征及奇函数性质可求a的范围;
②利用奇函数性质及单调递减性质可去掉不等式中的符号“f”,进而可转化为函数最值问题处理.
点评:本题考查函数的奇偶性、单调性及其应用,考查不等式恒成立问题,考查学生分析问题解决问题的能力.

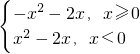 .
.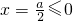 ,所以f(x)=-x2+ax在[0,+∞)上单调递减,
,所以f(x)=-x2+ax在[0,+∞)上单调递减, )递增,在(
)递增,在( ,+∞)上递减,不合题意,
,+∞)上递减,不合题意,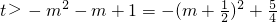 恒成立,所以
恒成立,所以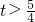 .
. ,+∞).
,+∞).

 已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为
已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为