
【题目】若当x∈R时,函数f(x)=a|x|始终满足0<|f(x)|≤1,则函数y=loga| ![]() |的图象大致为( )
|的图象大致为( )
A.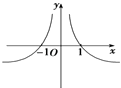
B.
C.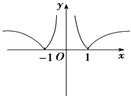
D.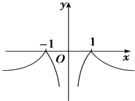
科目:高中数学 来源: 题型:
【题目】已知a,b,x,y∈R,证明:(a2+b2)(x2+y2)≥(ax+by)2 , 并利用上述结论求(m2+4n2)( ![]() +
+ ![]() )的最小值(其中m,n∈R且m≠0,n≠0).
)的最小值(其中m,n∈R且m≠0,n≠0).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:x∈R,x﹣2>lgx,命题q:x∈R,x2>0,则( )
A.命题p∨q是假命题
B.命题p∧q是真命题
C.命题p∧(¬q)是真命题
D.命题p∨(¬q)是假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A城市的出租车计价方式为:若行程不超过3千米,则按“起步价”10元计价;若行程超过3千米,则之后2千米以内的行程按“里程价”计价,单价为1.5元/千米;若行程超过5千米,则之后的行程按“返程价”计价,单价为2.5元/千米.设某人的出行行程为x千米,现有两种乘车方案:①乘坐一辆出租车;②每5千米换乘一辆出租车.
(Ⅰ)分别写出两种乘车方案计价的函数关系式;
(Ⅱ)对不同的出行行程,①②两种方案中哪种方案的价格较低?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:“直线x+y﹣m=0与圆(x﹣1)2+y2=1相交”;q:“方程mx2﹣2x+1=0有实数解”.若“p∨q”为真,“¬q”为假,则实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F为抛物线C:y2=4x的焦点,点P是准线l上的动点,直线PF交抛物线C于A,B两点,若点P的纵坐标为m(m≠0),点D为准线l与x轴的交点. (Ⅰ)求直线PF的方程;
(Ⅱ)求△DAB的面积S范围;
(Ⅲ)设 ![]() ,
, ![]() ,求证λ+μ为定值.
,求证λ+μ为定值.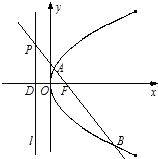
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆 ![]() 过点
过点 ![]() ,离心率为
,离心率为 ![]() ,左、右焦点分别为F1 , F2 , 过F1的直线交椭圆于A,B两点. (Ⅰ)求椭圆C的方程;
,左、右焦点分别为F1 , F2 , 过F1的直线交椭圆于A,B两点. (Ⅰ)求椭圆C的方程;
(Ⅱ)当△F2AB的面积为 ![]() 时,求直线的方程.
时,求直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为大力提倡“厉行节约,反对浪费”,某市通过随机询问100名性别不同的居民是否做到“光盘”行动,得到如下列联表及附表: 经计算: ![]()
做不到“光盘”行动 | 做到“光盘”行动 | |
男 | 45 | 10 |
女 | 30 | 15 |
P(X2≥x0) | 0.10 | 0.05 | 0.025 |
x0 | 2.706 | 3.841 | 5.024 |
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过1%的前提下,认为“该市民能否做到‘光盘’行动与性别有关”
B.在犯错误的概率不超过1%的前提下,认为“该市民能否做到‘光盘’行动与性别无关”
C.有90%以上的把握认为“该市民能否做到‘光盘’行动与性别有关”
D.有90%以上的把握认为“该市民能否做到‘光盘’行动与性别无关”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com