已知函数f(x)是定义域为(-1,1)上的奇函数也是减函数
(1)若x∈(-1,0)时,f(x)=-x+1,求f(x);
(2)若f(1-a)<f(a2-1),求a的取值范围.
解:(1)设x∈(0,1),则-x∈(-1,0),
由x∈(-1,0)时,f(x)=-x+1,得f(-x)=x+1,
又f(x)为(-1,1)上的奇函数,
所以f(-x)=-f(x),则-f(x)=x+1,
故f(x)=-x-1;
因为f(x)为(-1,1)上的奇函数,
所以f(-0)=-f(0),即f(0)=0,
所以f(x)=
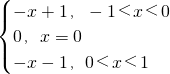
.
(2)因为f(x)为(-1,1)上的减函数,且f(1-a)<f(a
2-1),
所以有
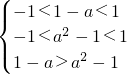
,解得0<a<1.
故a的取值范围是:0<a<1.
分析:(1)设x∈(0,1),则-x∈(-1,0),根据已知表达式可求得f(-x),由奇函数性质可得f(-x)与f(x)的关系,从而可求得f(x);由f(-0)=-f(0)可求得f(0),从而可得结论;
(2)利用函数f(x)的单调性可去掉不等式f(1-a)<f(a
2-1)中的符号“f”,从而转化为具体不等式,考虑到函数定义域,可得一不等式组,由此可得答案.
点评:本题考查函数的奇偶性、单调性及其应用,属中档题,定义是解决该类问题的基本方法,解决(2)问的关键是利用单调性化抽象不等式为具体不等式.

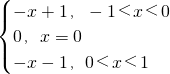 .
.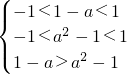 ,解得0<a<1.
,解得0<a<1.

 已知函数f(x)=x+
已知函数f(x)=x+