
【题目】将直角三角形![]() 沿斜边上的高
沿斜边上的高![]() 折成
折成![]() 的二面角,已知直角边
的二面角,已知直角边![]() ,那么下面说法正确的是( )
,那么下面说法正确的是( )
A. 平面![]() 平面
平面![]() B. 四面体
B. 四面体![]() 的体积是
的体积是![]()
C. 二面角![]() 的正切值是
的正切值是![]() D.
D. ![]() 与平面
与平面![]() 所成角的正弦值是
所成角的正弦值是![]()
【答案】C
【解析】
先由图形的位置关系得到![]() 是二面角
是二面角![]() 的平面角,
的平面角,![]() ,故A不正确;B由于
,故A不正确;B由于![]() 故得到B错误;易知
故得到B错误;易知![]() 为二面角
为二面角![]() 的平面角,
的平面角,![]() ,由题意可知∠BDC为B﹣AD﹣C的平面角,即∠BDC=120°,作DF⊥BC于F,连结AF,sin∠BCO=
,由题意可知∠BDC为B﹣AD﹣C的平面角,即∠BDC=120°,作DF⊥BC于F,连结AF,sin∠BCO=![]() .
.
沿![]() 折后如图,
折后如图,
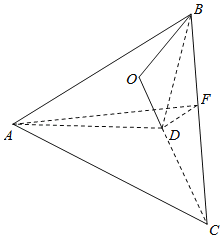
![]() ,易知
,易知![]() 是二面角
是二面角![]() 的平面角,
的平面角,
![]() ,
,![]() 由余弦定理得
由余弦定理得![]()
![]() ,可得
,可得![]() ,过
,过![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,则
,则![]() ,由面积相等得
,由面积相等得![]() ,可得
,可得![]() .
.
根据![]() ,易知
,易知![]() 是二面角
是二面角![]() 的平面角,
的平面角, ![]() 故A 平面
故A 平面![]() 与平面
与平面![]() 不垂直,
不垂直,![]() 错;
错;
B由于![]() ,
,![]() 错;
错;
C易知![]() 为二面角
为二面角![]() 的平面角,
的平面角,![]() ,
,![]() 对;
对;
D故如图,由题意可知∠BDC为B﹣AD﹣C的平面角,即∠BDC=120°,作DF⊥BC于F,连结AF,AF=![]() ,BD=4,DC=8,AD=4,过O作BO垂直BO⊥CO于O,则∠BCO就是BC与平面ACD所成角,BO=2
,BD=4,DC=8,AD=4,过O作BO垂直BO⊥CO于O,则∠BCO就是BC与平面ACD所成角,BO=2![]() ,OD=2,BC=
,OD=2,BC=![]() ,sin∠BCO=
,sin∠BCO=![]() .
.
选![]()


科目:高中数学 来源: 题型:
【题目】中国古代数学著作《算法统综》中有这样的一个问题:“三百七十八里关,初步健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还”.其大意为:“有一个人走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地”,请问此人第2天走的路程为
A. 24里 B. 48里 C. 72里 D. 96里
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2mx+2lnx,m∈R.
(1)探究函数f(x)的单调性;
(2)若关于x的不等式f(x)≤2![]() +3x2在(0,+∞)上恒成立,求m的取值范围.
+3x2在(0,+∞)上恒成立,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某射击运动员进行射击训练,前三次射击在靶上的着弹点![]() 刚好是边长为
刚好是边长为![]() 的等边三角形的三个顶点.
的等边三角形的三个顶点.

(Ⅰ)第四次射击时,该运动员瞄准![]() 区域射击(不会打到
区域射击(不会打到![]() 外),则此次射击的着弹点距
外),则此次射击的着弹点距![]() 的距离都超过
的距离都超过![]() 的概率为多少?(弹孔大小忽略不计)
的概率为多少?(弹孔大小忽略不计)
(Ⅱ) 该运动员前三次射击的成绩(环数)都在区间![]() 内,调整一下后,又连打三枪,其成绩(环数)都在区间
内,调整一下后,又连打三枪,其成绩(环数)都在区间![]() 内.现从这
内.现从这![]() 次射击成绩中随机抽取两次射击的成绩(记为
次射击成绩中随机抽取两次射击的成绩(记为![]() 和
和![]() )进行技术分析.求事件“
)进行技术分析.求事件“![]() ”的概率.
”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列的![]() 公差
公差![]() 不为0,
不为0,![]() 是其前
是其前![]() 项和,给出下列命题:
项和,给出下列命题:
①若![]() ,且
,且![]() ,则
,则![]() 和
和![]() 都是
都是![]() 中的最大项;
中的最大项;
②给定![]() ,对一切
,对一切![]() ,都有
,都有![]() ;
;
③若![]() ,则
,则![]() 中一定有最小项;
中一定有最小项;
④存在![]() ,使得
,使得![]() 和
和![]() 同号.
同号.
其中正确命题的个数为( )
A.4B.3C.2D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地草场出现火灾,火势正以每分钟![]() 的速度顺风蔓延,消防站接到警报立即派消防队员前去,在火灾发生后
的速度顺风蔓延,消防站接到警报立即派消防队员前去,在火灾发生后![]() 分钟到达救火现场,已知消防队员在现场平均每人每分钟灭火
分钟到达救火现场,已知消防队员在现场平均每人每分钟灭火![]() ,所消耗的灭火材料、劳务津贴等费用为每人每分钟
,所消耗的灭火材料、劳务津贴等费用为每人每分钟![]() 元,另附加每次救火所耗损的车辆、器械和装备等费用平均每人100元,而烧毁一平方米森林损失费为30元.
元,另附加每次救火所耗损的车辆、器械和装备等费用平均每人100元,而烧毁一平方米森林损失费为30元.
(1)设派![]() 名消防队员前去救火,用
名消防队员前去救火,用![]() 分钟将火扑灭,试建立
分钟将火扑灭,试建立![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)问应该派多少消防队员前去救火,才能使总损失最少?(注:总损失费=灭火劳务津贴+车辆、器械装备费+森林损失费)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知底角为![]() 的等腰梯形
的等腰梯形![]() ,底边
,底边![]() 长为7
长为7![]() ,腰长为
,腰长为![]() ,当一条垂直于底边
,当一条垂直于底边![]() 垂足为
垂足为![]() 的直线
的直线![]() 由
由![]() 从左至右向
从左至右向![]() 移动(与梯形
移动(与梯形![]() 有公共点)时,直线
有公共点)时,直线![]() 把梯形分成两部分,令
把梯形分成两部分,令![]()
![]() ,记左边部分的面积为
,记左边部分的面积为![]() .
.

(1)试求![]() 1,
1,![]() 3时的
3时的![]() 值;
值;
(2)写出![]() 关于
关于![]() 的函数关系式.
的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com