
分析 由条件求得c的值,利用余弦定理求得b的值,再利用正弦定理可得△ABC的外接圆的直径2R 的值.
解答 解:ABC中,∵a=1,B=45°,S△ABC=$\frac{1}{2}$ac•sinB=$\frac{a}{2}$•c•$\frac{\sqrt{2}}{2}$=2,∴c=4$\sqrt{2}$.
利用余弦定理可得b=$\sqrt{{a}^{2}{+c}^{2}-2ac•cosB}$=5,
再利用正弦定理可得△ABC的外接圆的直径2R=$\frac{b}{sinB}$=$\frac{5}{\frac{\sqrt{2}}{2}}$=5$\sqrt{2}$,
故答案为:$5\sqrt{2}$.
点评 本题主要考查正弦定理、余弦定理的应用,属于基础题.


科目:高中数学 来源: 题型:解答题
| 几何题 | 代数题 | 总计 | |
| 男同学 | 22 | 8 | 30 |
| 女同学 | 8 | 12 | 20 |
| 总计 | 30 | 20 | 50 |
| P(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
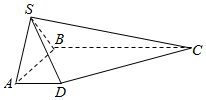 如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AB垂直于AD和BC,平面SAB⊥底面ABCD,且SA=SB=$\sqrt{2}$,AD=1,AB=2,BC=3.
如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AB垂直于AD和BC,平面SAB⊥底面ABCD,且SA=SB=$\sqrt{2}$,AD=1,AB=2,BC=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
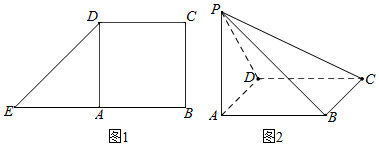
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | (?p)∧q | C. | p∧(?q) | D. | (?p)∧(?q) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com