
【题目】已知椭圆![]() :
:![]()
![]() 的左焦点为
的左焦点为![]() ,上顶点为
,上顶点为![]() ,长轴长为
,长轴长为![]() ,
,![]() 为直线
为直线![]() :
:![]() 上的动点,
上的动点,![]() ,
,![]() .当
.当![]() 时,
时,![]() 与
与![]() 重合.
重合.
(1)若椭圆![]() 的方程;
的方程;
(2)若直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,若
两点,若![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() (2) m=±1
(2) m=±1
【解析】试题分析:(1)根据题意得到由AF⊥BF得kAF·kBF=-1,进而求出椭圆方程;(2)由AP⊥AQ得,|AM|2=|PM|·|QM|,联立直线BM和椭圆得到二次方程,由韦达定理得到|PM|·|QM|的表达式,|AM|2=2+![]() ,两式相等即可.
,两式相等即可.
解析:
(Ⅰ)依题意得A(0,b),F(-c,0),当AB⊥l时,B(-3,b),
由AF⊥BF得kAF·kBF= ![]() ·
·![]() =-1,又b2+c2=6.
=-1,又b2+c2=6.
解得c=2,b=![]() .
.
所以,椭圆Γ的方程为![]() +
+![]() =1.
=1.
(Ⅱ)由(Ⅰ)得A(0,![]() ),依题意,显然m≠0,所以kAM=-
),依题意,显然m≠0,所以kAM=-![]() ,
,
又AM⊥BM,所以kBM=![]() ,所以直线BM的方程为y=
,所以直线BM的方程为y=![]() (x-m),
(x-m),
设P(x1,y1),Q(x2,y2).
y=![]() (x-m)与
(x-m)与![]() +
+![]() =1联立得(2+3m2)x2-6m3x+3m4-12=0,
=1联立得(2+3m2)x2-6m3x+3m4-12=0,
x1+x2=![]() ,x1x2=
,x1x2=![]() .
.
|PM|·|QM|=(1+![]() )|(x1-m)(x2-m)|
)|(x1-m)(x2-m)|
=(1+![]() )|x1x2-m(x1+x2)+m2|
)|x1x2-m(x1+x2)+m2|
=(1+![]() )·
)·![]()
=![]() ,
,
|AM|2=2+m2,
由AP⊥AQ得,|AM|2=|PM|·|QM|,
所以![]() =1,解得m=±1.
=1,解得m=±1.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),在以坐标原点为极点,
),在以坐标原点为极点,![]() 轴非负轴为极轴的极坐标系中,曲线
轴非负轴为极轴的极坐标系中,曲线![]() :
:![]() (
(![]() 为极角).
为极角).
(1)将曲线![]() 化为极坐标方程,当
化为极坐标方程,当![]() 时,将
时,将![]() 化为直角坐标方程;
化为直角坐标方程;
(2)若曲线![]() 与
与![]() 相交于一点
相交于一点![]() ,求
,求![]() 点的直角坐标使
点的直角坐标使![]() 到定点
到定点![]() 的距离最小.
的距离最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机构组织语文、数学学科能力竞赛,按照一定比例淘汰后,颁发一二三等奖.现有某考场的两科考试成绩数据统计如下图所示,其中数学科目成绩为二等奖的考生有![]() 人.
人.
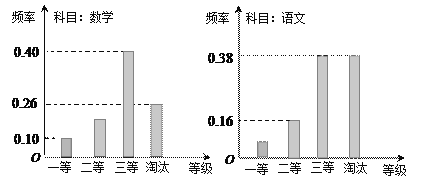

(Ⅰ)求该考场考生中语文成绩为一等奖的人数;
(Ⅱ)用随机抽样的方法从获得数学和语文二等奖的学生中各抽取![]() 人,进行综合素质测试,将他们的综合得分绘成茎叶图,求样本的平均数及方差并进行比较分析;
人,进行综合素质测试,将他们的综合得分绘成茎叶图,求样本的平均数及方差并进行比较分析;
(Ⅲ)已知本考场的所有考生中,恰有![]() 人两科成绩均为一等奖,在至少一科成绩为一等奖的考生中,随机抽取
人两科成绩均为一等奖,在至少一科成绩为一等奖的考生中,随机抽取![]() 人进行访谈,求两人两科成绩均为一等奖的概率.
人进行访谈,求两人两科成绩均为一等奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线![]() ,
,![]() ,
,![]() 为抛物线的焦点,
为抛物线的焦点,![]() 是抛物线上两点,线段
是抛物线上两点,线段![]() 的中垂线交
的中垂线交![]() 轴于
轴于![]() ,
,![]() ,
,![]() 。
。
(Ⅰ)证明:![]() 是
是![]() 的等差中项;
的等差中项;
(Ⅱ)若![]() ,
,![]() 为平行于
为平行于![]() 轴的直线,其被以AD为直径的圆所截得的弦长为定值,求直线
轴的直线,其被以AD为直径的圆所截得的弦长为定值,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆与圆![]() 相切,且与圆
相切,且与圆![]() 相内切,记圆心的轨迹为曲线.
相内切,记圆心的轨迹为曲线.
(Ⅰ)求曲线C的方程;
(Ⅱ)设Q为曲线C上的一个不在轴上的动点,O为坐标原点,过点![]() 作OQ的平行线交曲线C于M,N两个不同的点, 求△QMN面积的最大值.
作OQ的平行线交曲线C于M,N两个不同的点, 求△QMN面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨)标准煤的几组对照数据:
(吨)标准煤的几组对照数据:
![]()
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该厂技改前,100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
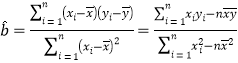 ,参考数值:
,参考数值:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com