设A,B,C是y=x2上的三点,其中B(1,1),且∠ABC=90°,过A,C分别作y=x2的切线,设两切线交于点M.
(1)求M点的轨迹方程;
(2)求证:直线AM、AC、CM的斜率kAM,kAC,kCM成等差数列.
解:(1)设A(x
1,x
12),C(x
2,x
22)
由AB⊥BC得K
AB•K
BC=-1
即
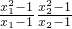
=-1
整理得:(x
1+1)(x
2+1)=-1,
x
1x
2+(x
1+x
2)+2=0(1)
又∵K
AM=2x
1,K
CM=2x
2∴直线AM的方程为:y-x
12=2x
1(x-x
1)(2)
直线CM的方程为:y-x
22=2x
2(x-x
2)(3)
联立(2),(3)解得M
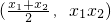
设M(x,y),则
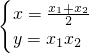
即
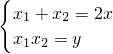
代入(1)得
点M的轨迹方程为:2x+y+2=0(7分)
(2)∵K
AM=2x
1,K
CM=2x
2∴K
AM+K
CM=2(x
1+x
2)
又∵K
AC=
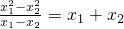
∴K
AM+K
CM=2K
AC即K
AM,K
AC,K
CM成等差数列.(15分)
分析:(1)先设A(x
1,x
12),C(x
2,x
22),由AB⊥BC得K
AB•K
BC=-1,再利用坐标表示它,整理得x
1与x
2的关系,再联立直线AM的方程和直线CM的方程,即得点M的轨迹方程;
(2)欲证明K
AM,K
AC,K
CM成等差数列,即证明K
AM,K
AC,K
CM成等差数列,利用K
AM=2x
1,K
CM=2x
2及K
AM+K
CM=2(x
1+x
2)即可证明得.
点评:本小题主要考查轨迹方程、等差数列、分析法和综合法等基础知识,考查运算求解能力、化归与转化思想.属于中档题.

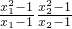 =-1
=-1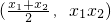
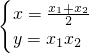 即
即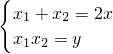 代入(1)得
代入(1)得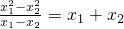


 选做题(在A、B、C、D四小题中只能选做两题,并将选作标记用2B铅笔涂黑,每小题10分,共20分,请在答题指定区域内作答,解答时应写出文字说明、证明过程或演算步骤).
选做题(在A、B、C、D四小题中只能选做两题,并将选作标记用2B铅笔涂黑,每小题10分,共20分,请在答题指定区域内作答,解答时应写出文字说明、证明过程或演算步骤).![]() 是坐标原点,如果
是坐标原点,如果![]() ,那么点(x,y)的轨迹是( )
,那么点(x,y)的轨迹是( )