练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    请你设计一个包装盒，如图所示，ABCD是边长为60 cm的正方形硬纸片，切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起，使得A，B，C，D四个点重合于图中的点P，正好形成一个正四棱柱形状的包装盒，E，F在AB上，是被切去的一个等腰直角三角形，斜边的两个端点，设AE＝FB＝x(cm)．

    ①某广告商要求包装盒的侧面积S(cm2)最大，试问x应取何值？
    ②某厂商要求包装盒的容积V(cm3)最大，试问x应取何值？并求出此时包装盒的高与底面边长的比值．

    ①x＝15②

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    已知函数f（x）＝lnx－a2x2＋ax（a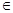R）.
    （l）当a＝1时，证明：函数f（x）只有一个零点；
    （2）若函数f(x)在区间（1，十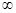）上是减函数，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数，其中.
    （Ⅰ）当时，求曲线在点处的切线方程；
    （Ⅱ）求f（x）的单调区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数f(x)＝(x2＋ax－2a2＋3a)ex(x∈R)，其中a∈R.
    (1)当a＝0时，求曲线y＝f(x)在点(1，f(1))处的切线的斜率；
    (2)当a≠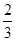时，求函数f(x)的单调区间与极值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数f(x)＝－x3＋ax2－4(a∈R)．
    (1)若函数y＝f(x)的图象在点P(1，f(1))处的切线的倾斜角为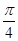，求f(x)在[－1,1]上的最小值；
    (2)若存在x0∈(0，＋∞)，使f(x0)＞0，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知a，b为常数，且a≠0，函数f(x)＝－ax＋b
    ＋axln x，f(e)＝2.
    ①求b；②求函数f(x)的单调区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数f(x)＝ln x＋ax(a∈R)．
    (1)求f(x)的单调区间；
    (2)设g(x)＝x2－4x＋2，若对任意x1∈(0，＋∞)，均存在x2∈[0,1]，使得f(x1)＜g(x2)，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数．
    （1）求在上的最大值；
    （2）若直线为曲线的切线，求实数的值；
    （3）当时，设，且，若不等式恒成立，求实数的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    直线l：y＝x＋a(a≠0)和曲线C：y＝x3－x2＋1相切，求切点
    的坐标及a的值．

    查看答案和解析>>

    同步练习册答案