
【题目】2020年初,新型冠状病毒肺炎(COVID-19)在我国爆发,全国人民团结一心、积极抗疫,为全世界疫情防控争取了宝贵的时间,积累了丰富的经验.某研究小组为了研究某城市肺炎感染人数的增长情况,在官方网站.上搜集了7组数据,并依据数据制成如下散点图:
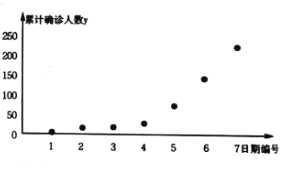
图中![]() 表示日期代号(例如2月1日记为“1”,2月2日记为“2”,以此类推).通过对散点图的分析,结合病毒传播的相关知识,该研究小组决定用指数型函数模型
表示日期代号(例如2月1日记为“1”,2月2日记为“2”,以此类推).通过对散点图的分析,结合病毒传播的相关知识,该研究小组决定用指数型函数模型![]() 来拟合,为求出
来拟合,为求出![]() 关于
关于![]() 的回归方程,可令
的回归方程,可令![]() ,则
,则![]() 与
与![]() 线性相关.初步整理后,得到如下数据:
线性相关.初步整理后,得到如下数据:![]() ,
,![]() .
.
(1)根据所给数据,求出![]() 关于
关于![]() 的线性回归方程:
的线性回归方程:
(2)求![]() 关于
关于![]() 的回归方程;若防控不当,请问
的回归方程;若防控不当,请问![]() 为何值时,累计确诊人数的预报值将超过1000人?(参考数据:
为何值时,累计确诊人数的预报值将超过1000人?(参考数据:![]() ,结果保留整数)
,结果保留整数)
附:对于一组数据![]() ,其线性回归方程
,其线性回归方程![]() 的斜率和截距的最小二乘估计公式分别为
的斜率和截距的最小二乘估计公式分别为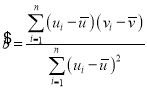 ,
,![]() .
.
科目:高中数学 来源: 题型:
【题目】算盘是中国传统的计算工具,其形长方,周为木框,内贯直柱,俗称“档”,档中横以梁,梁上两珠,每珠作数五,梁下五珠,每珠作数一.算珠梁上部分叫上珠,梁下部分叫下珠.例如:在十位档拨上一颗上珠和一颗下珠,个位档拨上一颗上珠,则表示数字65.若在个、十、百、千位档中随机选择一档拨一颗上珠,再随机选择两个档位各拨一颗下珠,则所拨数字大于200的概率为( ).

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如图,则下面结论中错误的一个是( )

A. 甲的极差是29 B. 甲的中位数是24
C. 甲罚球命中率比乙高 D. 乙的众数是21
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】整数集就像一片浩瀚无边的海洋,充满了无尽的奥秘.古希腊数学家毕达哥拉斯发现220和284具有如下性质:220的所有真因数之和恰好等于284,同时284的所有真因数之和也等于220,他把具有这种性质的两个整数叫做一对“亲和数”,“亲和数”的发现吸引了古今中外无数数学爱好者的研究热潮.已知220和284,1184和1210,2924和2620是3对“亲和数”,把这六个数随机分成两组,一组2个数,另一组4个数,则220和284在同一组的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列选项中说法正确的是( )
A.函数![]() 的单调减区间为
的单调减区间为![]() ;
;
B.命题“![]() ”的否定是“
”的否定是“![]() ”;
”;
C.在三角形![]() 中,“若
中,“若![]() ,则
,则![]() ”的逆否命题是真命题
”的逆否命题是真命题
D.幂函数![]() 过点
过点 ,则
,则![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com