
【题目】如图长方体![]() 中,
中,![]() ,
,![]() 分别为棱
分别为棱![]() ,
,![]() 的中点
的中点

(1)求证:平面![]() 平面
平面![]() ;
;
(2)请在答题卡图形中画出直线![]() 与平面
与平面![]() 的交点
的交点![]() (保留必要的辅助线),写出画法并计算
(保留必要的辅助线),写出画法并计算![]() 的值(不必写出计算过程).
的值(不必写出计算过程).
【答案】(1)见证明;(2) ![]() ;画图见解析
;画图见解析
【解析】
(1)推导出![]() 平面
平面![]() ,得出
,得出![]() ,得出
,得出![]() ,从而得到
,从而得到![]() ,进而证出
,进而证出![]() 平面
平面![]() ,由此证得平面
,由此证得平面![]() 平面
平面![]() .
.
(2)根据通过辅助线推出线面平行再推出线线平行,再根据“一条和平面不平行的直线与平面的公共点即为直线与平面的交点”得到![]() 点位置,然后计算
点位置,然后计算![]() 的值.
的值.
(1)证明:在长方体![]() 中,
中,![]() ,
,
![]() 分别为棱
分别为棱![]() ,
,![]() 的中点,所以
的中点,所以![]() 平面
平面![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,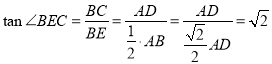 ,
,
所以![]() ,因为在
,因为在![]() 中,
中,![]() ,所以
,所以![]() ,所以
,所以![]() ,又因为
,又因为![]() ,所以
,所以![]() 平面
平面![]() ,因为
,因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]()
(2)
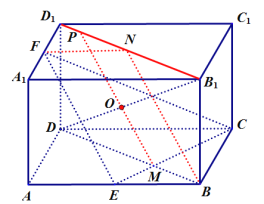
如图所示:设![]() ,连接
,连接![]() ,取
,取![]() 中点记为
中点记为![]() ,过
,过![]() 作
作![]() ,且
,且![]() ,则
,则![]() .
.
证明:因为![]() 为
为![]() 中点,所以
中点,所以![]() 且
且![]() ;又因为
;又因为![]() ,且
,且![]() ,所以
,所以![]() 且
且![]() ,所以四边形
,所以四边形![]() 为平行四边形,则
为平行四边形,则![]() ;又因为
;又因为![]() ,所以
,所以![]() ,且
,且![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ;又因为
;又因为![]() ,则
,则![]() ,
,![]() 平面
平面![]() ,即点
,即点![]() 为直线
为直线![]() 与平面
与平面![]() 的交点;
的交点;
因为![]() ,所以
,所以![]() ,则
,则![]() ;且有上述证明可知:四边形
;且有上述证明可知:四边形![]() 为平行四边形,所以
为平行四边形,所以![]() ,所以
,所以![]() ,
,
因为![]() ,
,![]() .
.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:
【题目】若对任意x∈(0,π),不等式ex﹣e﹣x>asinx恒成立,则实数a的取值范围是( )
A.[﹣2,2]
B.(﹣∞,e]
C.(﹣∞,2]
D.(﹣∞,1]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() 满足:对任意的实数
满足:对任意的实数![]() ,存在非零常数
,存在非零常数![]() ,都有
,都有![]() 成立.
成立.
(1)当![]() 时,若
时,若![]() ,
, ![]() ,求函数
,求函数![]() 在闭区间
在闭区间![]() 上的值域;
上的值域;
(2)设函数![]() 的值域为
的值域为![]() ,证明:函数
,证明:函数![]() 为周期函数.
为周期函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=m﹣|2﹣x|,且f(x+2)>0的解集为(﹣1,1).
(1)求m的值;
(2)若正实数a,b,c,满足a+2b+3c=m.求 ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 对一切实数
对一切实数![]() 都有
都有![]() 成立,且
成立,且![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 的解析式,并用定义法证明
的解析式,并用定义法证明![]() 在
在![]() 单调递增;
单调递增;
(3)已知![]() ,设P:
,设P:![]() ,不等式
,不等式![]() 恒成立,Q:
恒成立,Q:![]() 时,
时,![]() 是单调函数。如果满足P成立的
是单调函数。如果满足P成立的![]() 的集合记为A,满足Q成立的
的集合记为A,满足Q成立的![]() 集合记为B,求
集合记为B,求![]() (R为全集)。
(R为全集)。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣![]() .
.
(1)若a>0,试判断f(x)在定义域内的单调性;
(2)若f(x)在[1,e]上的最小值为![]() ,求实数a的值;
,求实数a的值;
(3)若f(x)<x2在(1,+∞)上恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】本小题12分)
调查某地区老年人是否需要志愿者帮助,用简单随机抽样方法从该地调查500位老年人,结果如下:
性别 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
①估计该地区老年人中,需要志愿者提供帮助的老年人的比例。
②能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
附:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com