
【题目】已知双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的左、右焦点分别是F1 , F2 , 过F2的直线交双曲线的右支于P,Q两点,若|PF1|=|F1F2|,且3|PF2|=2|QF2|,则该双曲线的离心率为( )
=1(a>0,b>0)的左、右焦点分别是F1 , F2 , 过F2的直线交双曲线的右支于P,Q两点,若|PF1|=|F1F2|,且3|PF2|=2|QF2|,则该双曲线的离心率为( )
A.![]()
B.![]()
C.2
D.![]()
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】对某校高二年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下: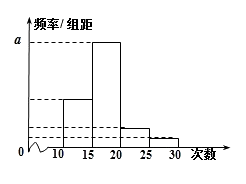

(1)求出表中M,P及图中 ![]() 的值;
的值;
(2)若该校高二学生有240人,试估计该校高二学生参加社区服务的次数在区间[10,15]内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间[25,30]内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若命题p:从有2件正品和2件次品的产品中任选2件得到都是正品的概率为三分之一;命题q:在边长为4的正方形ABCD内任取一点M,则∠AMB>90°的概率为 ![]() ,则下列命题是真命题的是( )
,则下列命题是真命题的是( )
A.p∧q
B.(p)∧q
C.p∧(q)
D.q
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=2 ![]() ,AD=
,AD= ![]() ,M为DC的中点,将△DAM沿AM折到△D′AM的位置,AD′⊥BM.
,M为DC的中点,将△DAM沿AM折到△D′AM的位置,AD′⊥BM. 
(1)求证:平面D′AM⊥平面ABCM;
(2)若E为D′B的中点,求二面角E﹣AM﹣D′的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,其中b≠c,且bcosB=ccosC,延长线段BC到点D,使得BC=4CD=4,∠CAD=30°, 
(Ⅰ)求证:∠BAC是直角;
(Ⅱ)求tan∠D的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知随圆E: ![]() +
+ ![]() =1(a>b>0)与过原点的直线交于A、B两点,右焦点为F,∠AFB=120°,若△AFB的面积为4
=1(a>b>0)与过原点的直线交于A、B两点,右焦点为F,∠AFB=120°,若△AFB的面积为4 ![]() ,则椭圆E的焦距的取值范围是( )
,则椭圆E的焦距的取值范围是( )
A.[2,+∞)
B.[4,+∞)
C.[2 ![]() ,+∞)
,+∞)
D.[4 ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京市2016年12个月的PM2.5平均浓度指数如图所示.由图判断,四个季度中PM2.5的平均浓度指数方差最小的是( ) 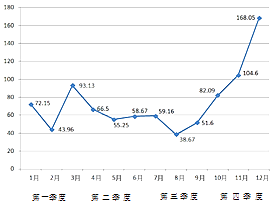
A.第一季度
B.第二季度
C.第三季度
D.第四季度
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com