
已知 的面积为1,点
的面积为1,点 在
在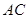 上,
上, ,连结
,连结 ,设
,设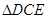 、
、 、
、 中面积最大者的值为
中面积最大者的值为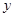 ,则
,则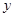 的最小值为 .
的最小值为 .

【解析】
试题分析:解:设CD:CA=k,则因为点D在AC上,所以0<k<1 ,∵DE∥AB,∴△DCE∽△ACB,∴S△DCE:S△ACB=(CD:CA)2=k2,∵S△ABC=1,∴S△DCE=k2;
,∵AD:AC=(AC-CD):AC=1-k,∴S△ABD:S△ABC=AD:AC=1-k,∴S△ABD=1-k,∵DE∥AB,∴CE:BE=CD:AD=k:(1-k) ,∵S△DCE:S△BDE=CE:BE=k:(1-k)∴S△BDE=[(1-k):k]×S△DCE=-k2+k,当k2=1-k时,k2+k-1=0,∴k=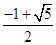 ;当k2=-k2+k时,2k2-k=0,∴k=
;当k2=-k2+k时,2k2-k=0,∴k= 当1-k=-k2+k时,k2-2k+1=0,∴k=1,故可知y=1-k,0<k≤
当1-k=-k2+k时,k2-2k+1=0,∴k=1,故可知y=1-k,0<k≤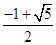 k2,
k2,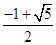 <k<1,故可知当k=
<k<1,故可知当k=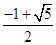 时,y有最小值
时,y有最小值
考点:三角形面积
点评:本题考查三角形面积的计算,考查函数的最值,考查分段函数,考查学生分析解决问题的能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:陕西省模拟题 题型:解答题
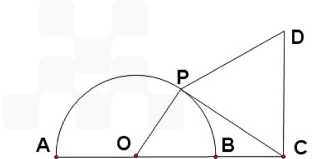
如图,已知 的半径是1,点在直径AB的延长线上, BC=1, 点P是
的半径是1,点在直径AB的延长线上, BC=1, 点P是 上半圆上的动点, 以PC为边作等边三角形PCD,且点D与圆心分别在PC的两侧.
上半圆上的动点, 以PC为边作等边三角形PCD,且点D与圆心分别在PC的两侧.
(Ⅰ) 若 ,试将四边形OPDC的面积y表示成θ的函数;
,试将四边形OPDC的面积y表示成θ的函数;
(Ⅱ) 求四边形OPDC的面积的最大值.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省苏州市五市三区高三(上)期中数学模拟试卷(一)(解析版) 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分13分)
 如图,已知
如图,已知![]() 的半径为1,点C在直径AB的延长线上,BC=1,点P是半圆上的一个动点,以PC为边作正三角形PCD,且点D
的半径为1,点C在直径AB的延长线上,BC=1,点P是半圆上的一个动点,以PC为边作正三角形PCD,且点D
与圆心分别在PC两侧.
(1)若![]() ,试将四边形OPDC的面积
,试将四边形OPDC的面积
y表示成![]() 的函数;
的函数;
(2)求四边形OPDC面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com